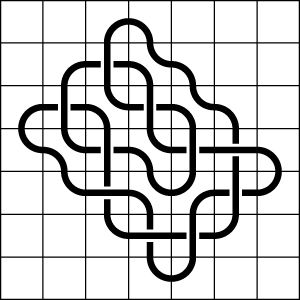
Knot Mosaics for the 1020 Knot

For many knots, the tile number and/or crossing number cannot be realized when the mosaic number is realized.

The mosaic of the 1020 knot given in the table has the mosaic number realized, which is 6, but the tile number and crossing number of this knot cannot be realized on a 6-mosaic. On a 6-mosaic, the fewest number of non-blank tiles needed to create this knot is 32. However, the tile number of this knot is 27, and this cannot be realized on anything smaller than a 7-mosaic. The crossing number is also first realized on a 7-mosaic, but at least 31 non-blank tiles are necessary to achieve it. Below are the relevant mosaics.

1020 with mosaic number realized.
1020 with tile number realized.
1020 with crossing number realized.

Back to the Knot Mosaic Table

References:

Heap, A.; Knowles, D. Tile Number and Space-Efficient Knot Mosaics; J. Knot Theory Ramif. 2018, 27.
Heap, A.; Knowles, D. Space-Efficient Knot Mosaics for Prime Knots with Mosaic Number 6; Involve 2019, 12.
Heap, A.; LaCourt, N. Space-Efficient Prime Knot 7-Mosaics; Symmetry 2020, 12.
Heap, A.; Baldwin, D.; Canning, J.; Vinal, G. Knot Mosaics For Prime Knots with Crossing Number 10 or Less; in preparation.

[Back to Top]