Problem Set 5—Proofs about Context Free Languages

Purpose

This problem set lets you review some important proofs about context free languages and pushdown automata, and practice proving things about them yourself. In particular, this problem set deals with (1) the proof that every context free grammar has a pushdown automaton that recognizes the same language, (2) the proof that every pushdown automaton has a context free grammar that generates the same language, and (3) the pumping lemma for context free languages.

Background

This problem set is based on material in sections 2.2 and 2.3 of our textbook. We discussed the equivalence of context free languages with the languages recognized by pushdown automata in class on February 24 and February 26. We will discuss the pumping lemma for context free languages on Feburary 29.

Activity

Solve each of the following problems.

Problem 1

In class on February 26 we used the following pushdown automaton as an example for constructing a grammar from a PDA:

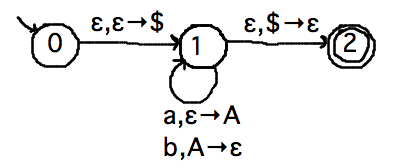
We claimed without proof that the following grammar generates the language of this PDA:

A₀₂ → A₁₁
A₁₁ → a A₁₁ b | ε | A₁₁ A₁₁

Finish using the construction from our textbook’s Lemma 2.27 to derive this grammar.

Problem 2

Use the construction from our textbook’s Lemma 2.21 to construct a pushdown automaton from the grammar given in Problem 1.

Problem 3

Problem 2.30d in our textbook (show that {t₁#t₂#…#t_n | t_i∈{a,b}* for all 1 ≤ i ≤ n and for some j and k, j ≠ k, t_j = t_k} is not context free).

Problem 4

Problem 2.32 in our textbook (show that the set of strings over {1,2,3,4} in which the number of 1s equals the number of 2s and the number of 3s equals the number of 4s is not context free).

Follow-Up

I will grade this exercise in a face-to-face meeting with you. During this meeting I will look at your solution, ask you any questions I have about it, answer questions you have, etc. Please bring a written solution to the exercise to your meeting, as that will speed the process along.

Sign up for a meeting via Google calendar. If you worked in a group on this exercise, the whole group should schedule a single meeting with me. Please make the meeting 15 minutes long, and schedule it to finish before the end of the “Grade By” date above.