- Colloquium
- “Is the Set of Knots Fractal?”
- Dr. Arunima Ray, Brandeis University (and Geneseo math alumna)
- Friday, Jan. 29, 2:45; Newton 204
- Extra credit (up to 1/5 of a homework) for going and writing ca 1 paragraph to 1 page on intellectual connections you make to the talk
- With (deterministic) finite automata as a model, how do you answer the question(s) “what does it mean to compute?”, “what is computation?”, etc.
- Computation = accepting or rejecting strings according to whether they are in a language or not
- To compute = go through series of DFA states according to transition function
- Section 1.2 through “Formal Definition…”
- Nondeterministic automata
- Can have multiple transitions for each state/symbol
- Automaton splits into multiple paths, each keeps running
- Or no arrows
- Branch dies
- Does branch die even if the state that lacks a transition is accepting?
- Yes, because that branch goes from the accepting state to no state
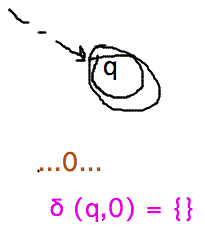
- Yes, because that branch goes from the accepting state to no state
- Or epsilon transitions: split and then reads input from both next states
- Deterministic special case of nondeterministic
- NFA easier to design than DFA
- NFA accepts if any branch ends in accepting state
- NFA trades parallelism for states
- Examples
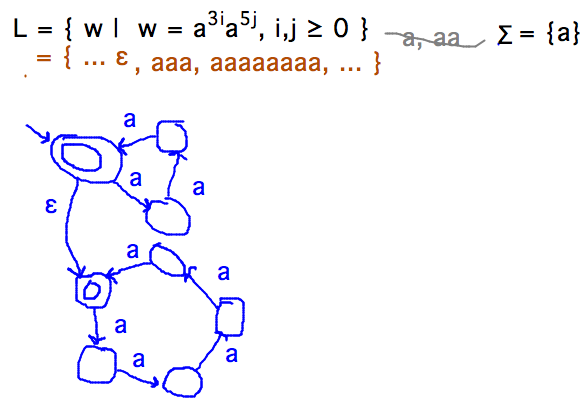
- NFA that recognizes strings over {a} with lengths of the form 3i + 5j,
i, j integers ≥ 0
- Show that NFAs don’t really need the ability to make more than 1 transition
per symbol as long as they can make 0 or 1 transitions and have ε
transitions
- Proof by construction

- Make such proofs rigorous by writing them in terms of formal definitions
- Also prove constructed and original machines accept same language
- Proof by construction
- NFA that recognizes strings over {a} with lengths of the form 3i + 5j,
i, j integers ≥ 0
- Problem Set
- NFAs are no more powerful than DFAs - any NFA can be converted to a DFA
- Read “Equivalence of NFAs and DFAs” part of section 1.2
- Bottom of page 54 through top 2/3 of page 58