SUNY Geneseo Department of Mathematics
Wednesday, April 10
Math 239 01
Spring 2019
Prof. Doug Baldwin
PRISM’s calculus bee is today (Wednesday), 2:30 - 3:45, Newton 201.
Sections 6.1 and 6.2
Suggest domain, codomain, and range of the following. Write using the “f : A → B” notation. Give examples of images and preimages.
f(x) = x + 1. Domain & codomain & range are reals. Image of 1 = f(1) = 2, so preimage of 2 is 1. This can be written as f : ℝ → ℝ. But note that there is nothing in the definition “f(x) = x + 1” that says the domain or codomain must be the reals — they could also both be the integers, the codomain could be any superset of the range (e.g., reals when the range was integers, etc.)
g(x) = x2+1. A preimage of 5 is 2 and also -2 — values can have multiple preimages. g : ℤ → ℕ, or domain is the set of imaginary numbers and range is the reals. Again, nothing in the statement of how to calculate the function uniquely defines the domain.
h(x) = √((x+1)/x). Domain is { x in ℝ | x > 0 }. Or { x in ℝ | x > 0 or x ≤ -1 }. And we get even more choices of domain if we allow imaginary numbers in the codomain. Note that each choice of a domain (and codomain) corresponds to a different function, even though both are calculated the same way.
Some functions defined by arrow diagrams — a nice visual way to see domain and codomain and the concept of “mapping.”
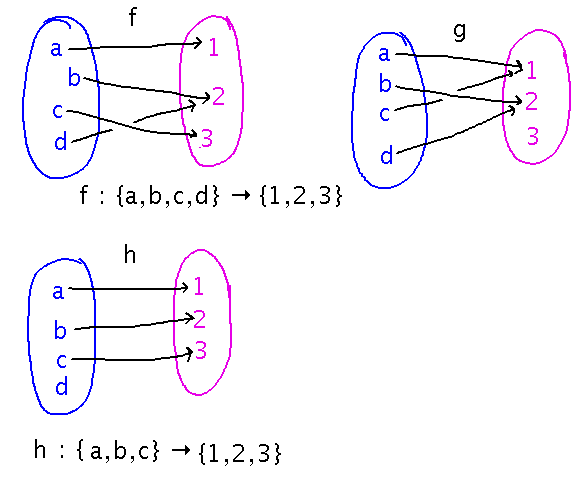
Notice that h here is either a function with the domain shown, or it’s not a function at all because the domain is meant to be {a,b,c,d} but h doesn’t map everything in that set.
Here are some examples of mappings. Do any of them have mathematically “nice” properties, and what makes a property “nice” anyhow?
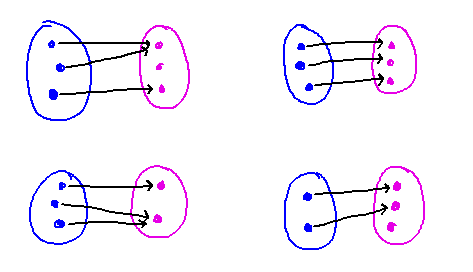
The upper right example is “nice” in that it maps the whole domain to the whole codomain, and everything in the codomain has a unique preimage. Mathematically, this is nice because it means an “inverse” function, i.e., a mapping from codomain back to domain that undoes the original mapping, is possible.
On the other hand, the lower right mapping that doesn’t map anything to some element of the codomain seems a little awkward, what we think of as a function more naturally maps to the whole codomain (i.e., range equals codomain).
A function is defined by a calculation/mapping AND a domain AND a codomain.
Functions MUST map every element of their domain.
Functions needn’t map to every element of their codomain (but must map to every element of their range).
Some special kinds of function — injections, surjections, and bijections.
Read section 6.3.