SUNY Geneseo Department of Mathematics
Friday, April 20
Math 239 01
Spring 2018
Prof. Doug Baldwin
... Finishing the proof from Wednesday.
Define the notation “x mod y,” for integers x and y, to mean the integer k such that x = qy + k for some integer q and 0 ≤ k < y. By Corollary 3.32, k is unique for any given x and y.
Suppose f : {0,1,...,999} → {0,1,...,999} is defined by f(n) = (n+100) mod 1000.
Also suppose g : {0,1,...,999} → {0,1,...,999} is defined by g(n) = (n+900) mod 1000.
Prove that g = f-1.
We argued Wednesday that for any functions f and g, g = f-1 if for all n in dom(g), f(g(n)) = n and for all m in dom(f), g(f(m)) = m.
Now do the proof about the specific f and g above.
We actually came up with several proofs.
One, which particularly cleanly captures ideas that a couple of people touched on, shows that if f(a) = b, then g(b) = a, and vice versa:
Proof 1. We show that if f and g are defined as above, then f(a) = b if and only if g(b) = a.
For the first direction, assume f(a) = b, so that
Applying the definition of “mod” given above and rearranging gives
for some integer x. Adding and then subtracting 1000 on the right side produces
or, by moving 900 + b and a to the other sides of the equation and then negating both sides,
Finally, applying the definition of “mod” to this last equation, we get
This establishes that if f(a) = b, then g(b) = a. The proof in the other direction is similar. Thus, f(a) = b if and only if g(b) = a. In terms of functions as ordered pairs, we have that the pair (a,b) is in f if and only if (b,a) is in g, and so g = f-1. QED.
Another approach gives piecewise definitions of f and g that are equivalent to the originals, namely
f(n) =
g(n) =
Now we can use these definitions to show that f(a) = b if and only if g(b) = a, as follows:
Proof 2. We use the piecewise definitions of f and g to prove that f(a) = b if and only if g(b) = a.
Suppose f(a) = b. There are 2 cases to consider, namely 0 ≤ a ≤ 899 and 900 ≤ a ≤ 999. In the first case, f(a) = a + 100. Noting that 100 ≤ a + 100 ≤ 999 in this case, g(f(a)) is f(a) - 100 = a + 100 - 100 = a. In the second case, f(a) = a - 900, and 0 ≤ a - 900 ≤ 99. Thus g(f(a)) is defined by the first part of g’s definition, namely g(f(a)) = f(a) + 900 = a - 900 + 900 = a. These two cases establish that if f(a) = b, then g(b) = a for all a in dom(f).
The proof in the other direction is similar. We thus see that f(a) = b if and only if g(b) = a, and so g = f-1. QED.
Proofs about functions and their inverses; often these use an element-chasing style of following a generic value through one or more functions.
Section 7.1.
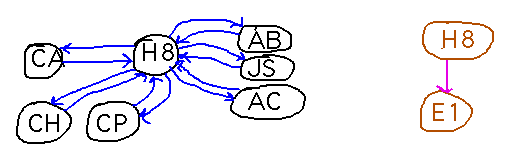
What “relations,” in a colloquial sense, do you see in Henry VIII’s family tree?
A daughter-of relation, e.g., Elizabeth I (E1) is the daughter of Henry VIII (H8), Elizabeth I is the daughter of Anne Boleyn (AB), Mary I (M1) is the daughter of Henry VIII, Mary I is the daughter of Catherine of Aragon (CA), etc.
We can represent these items as order pairs, e.g., (E1,H8), (E1,AB), (M1,H8), (M1,CA), etc.
There’s also a marriage relation, e.g., Henry VIII was married to Catherine of Aragon, who was also married to Henry VIII, etc.
As ordered pairs, (H8,CA), (CA, H8), ...
A relation between sets A and B is a subset of A × B.
Notions of domain, codomain, etc. apply to relations just like they do to functions.
A function is a kind of relation, but general relations don’t have the restrictions functions do, e.g., each element in the domain can be related to as many or as few elements of the codomain as you want.
A visual way to present relations (although also one with lots of mathematics in its own right). The idea is that each entity that appears in the relation is represented as a circle or dot (a “vertex”), with arrows (“edges”) between the entities that are related by the relation. For example, here are parts of the marriage (black vertices) and daughter (brown vertices) relations for Henry VIII’s family:
Equivalence relations.
Read section 7.2.