Set Algebra

Misc

Prof Aguilar is advertising for summer research students. This is a great opportunity to get involved in math from a different (and much more rewarding) perspective than that of a typical class. See flyers around the math department or Prof. Aguilar for more information.

Questions?

Set Algebra

Section 5.3.

Warm Up

Draw Venn diagrams that illustrate that (A∪B)^C = A^C ∩ B^C.

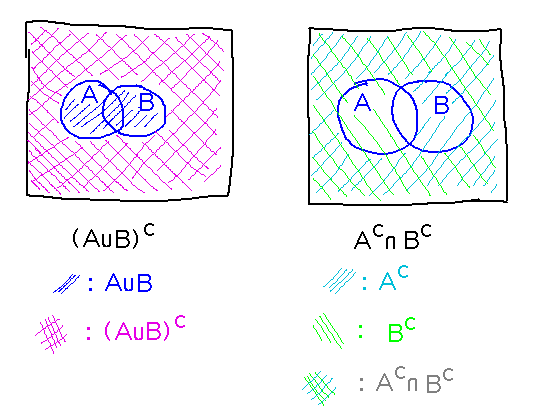
In Proofs

Prove that if A, B, and C are subsets of some universal set U, then A - (B-C) = (A-B) ∪ (A ∩ C).

Proof: We use the laws of set algebra to prove that if A, B, and C are subsets of some universal set U, then A - (B-C) = (A-B) ∪ (A ∩ C). In particular, we see that

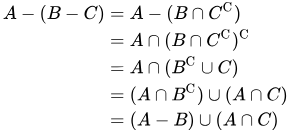
which establishes that A - (B-C) = (A-B) ∪ (A ∩ C). QED.

Exploratory

Does intersection distribute over set difference, i.e., is A ∩ (B-C) = A ∩ B - A ∩ C? If not, can you find some other equivalence for A ∩ (B-C)?

Some equivalences we found:

• A ∩ (B-C) = (A-B) ∪ (A-C)
• A ∩ B - A ∩ C = (A-B^C) - (A-C^C)
• A ∩ (B-C) = (A∩B) - C = B ∩ (A-C)

Addressing the main question about distributivity, we conjectured that intersection does distribute over difference, based on Venn diagrams and some other equivalences that seemed to address part of the main question. We were finally able to establish it formally, namely...

Theorem: if A, B, and C are subsets of some universal set, then A ∩ (B-C) = A ∩ B - A ∩ C.

Proof: We use the laws of set algebra to prove that if A, B, and C are subsets of some universal set, then A ∩ (B-C) = A ∩ B - A ∩ C. In particular, we work from the right side of the equation and see...

We have now shown that if A, B, and C are subsets of some universal set, then A ∩ (B-C) = A ∩ B - A ∩ C. QED.

Key Points

There is an algebra for set operations.

It’s useful in reasoning about (e.g., simplifying, proving equalities, etc.) expressions involving sets.

Next

Cartesian products of sets

Read section 5.4.