Questions Discussed in the Review Session
Families of Sets?
A family is just a set of sets; it’s often convenient to name the members of that set with indices.
For a small tangible example, A here is a family consisting of 3 sets:
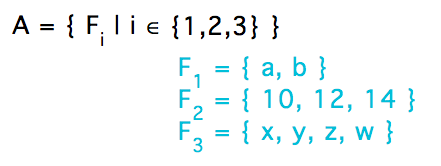
Families are often used in situations where you want to talk about operations on some or all members of the family. Indexing provides handy notation for talking about such operations. For example...

Cardinality?
Informally, cardinality is the size of a set
e.g., |{1,2,3,5}| = card( {1,2,3,5} ) = 4
How does this work for infinite sets where you can’t just count the elements?
- Define A and B to have the same cardinality if and only if there is a bijection from A to B. This is intuitively reasonable for finite sets, where an injection from A to B requires B to have at least as many elements as A so each element of A can map to a unique element of B, and being a surjection requires B to have no more elements than A, so that mapping from A can “fill” all of B, so being both an injection and a surjection requires A and B to have the same number of elements. And the concept of bijection extends easily to functions between infinite sets.
- A bijection from A to ℕk = {1,2,....,k} corresponds to A being a finite set of cardinality k.
- No such bijection for any k corresponds to A being infinite.
What is the point of the countably infinite hotel?
- Two points.
- First, to provide an accessible analog for the ideas in the proof that the union of two disjoint countably infinite sets is countably infinite, namely interleaving the elements of two sets in a way corresponding to odd and even natural numbers.
- Second, to drive home that “arithmetic” on infinite quantities doesn’t work like arithmetic on finite quantities, and that you really shouldn’t even think of infinities as numbers at all.
Cantor and “Dodge Ball”?
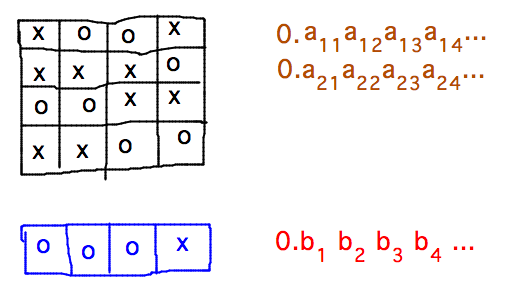
Player 2’s goal in the dodge ball game is to make a list of xs and os that is different from every list player 1 makes.
Cantor’s goal in his diagonalization proof is to make a real number different from every one in an alleged bijection from the naturals to (0,1).
Both use the same strategy, namely creating a sequence whose ith element differs in its ith position from the ith member of the list being avoided.
So dodge ball is basically Cantor’s diagonalization scaled down to finite sequences.
Induction Example
A rigorous proof that one of de Morgan’s laws scales up to any number of propositions.
(Note that the idea in the review session that induction could take this claim to any countable set of propositions isn’t quite right — induction can get you to any of the infinite number of naturals, but each of them is still a finite number. Induction does not extend to infinite cardinals, even countable ones. Which doesn’t mean our claim isn’t true for infinite sets of propositions, just that induction can’t prove it. The claim and proof below are rephrased to reflect this.)
