Misc
Online Course Survey
The Provost’s Technology Advisory Committee is interested in students’ experiences with online courses, whether as a taker of them or as a non-taker, and whether from Geneseo or other schools. You’re likely to get a request to fill out a survey on this subject. Please do so if you get the request.
Review Session
1:00 - 2:00 PM Wednesday (May 3, study day), in our regular room.
Final Exam
Wednesday, May 10, 12:00 noon
Comprehensive, but emphasizes material since second hour exam (e.g., set theory, functions, equivalence relations, infinite cardinalities, etc.)
Designed for about 1 1/2 hours, you’ll have 2 1/2.
There will be one closed-book question at the beginning of the test, then the rest will be open-book (and open-notes, open-computer, etc.)
Otherwise the rules and format will be similar to the hour exams.
I’ll bring donuts and cider.
SOFIs
3 responses as of last night — thank you to the three.
Questions?
Uncountable Sets
Section 9.3
Dodge Ball
Play it.
What is the winning strategy, and who wins?
- Player 2 wins by marking column i with the opposite of the mark player 1 made in row i, column i.
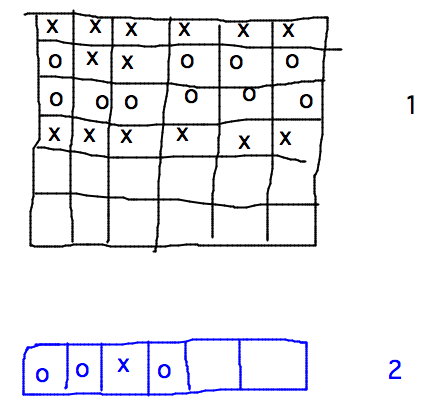
Example
Prove that the set of countably infinite sequences over {x,o} is uncountable.
Relevant ideas or questions from reading:
- Theorem 9.22, that (0,1) is uncountable.
- Proved by showing that no function from ℕ to (0,1) can be a surjection.
Proof.
- By contradiction.
- Assume there is a bijection f from ℕ to the set of countably infinite sequences over {x,o}
- Construct sequence B that’s not the image of any n in ℕ: Bi = x if f(i)i = o, Bi = o if f(i)i = x.
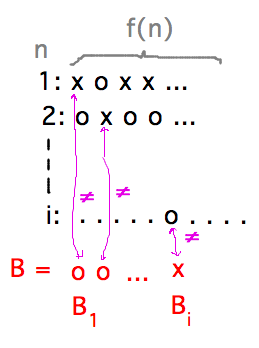
- So f is not a surjection onto the set of sequences, since there is at least one sequence that isn’t the image of any natural number.
- But this is a contradiction: f is a bijection by assumption, and so has to be a surjection.
Comments:
- You can prove that sets are uncountable either by diagonalization, as you did here, or by showing that they are equivalent to a set already known to be uncountable.
- This diagonalization is just an extension of the dodgeball strategy to infinite sequences.
Next
Some definitions (which you might remember from problem set 3):
- An alphabet is a finite set. The members of an alphabet are called symbols.
- If A is an alphabet, a string over A is a finite sequence of symbols from A.
How many strings are there over any finite alphabet?
Is the set of functions from ℕ to ℕ countable or uncountable?
Which are there “more” of, things you might want to calculate with a computer program, or computer programs to calculate them? (A little more accurately, is it possible to associate a distinct program with each thing you might want to calculate with a program?)