Misc
Canvas Trouble?
Is anyone not able to see the lecture notes from Friday or today?
Calculus Bee
Wednesday, April 19, 2:45 PM, Newton 204
Colloquium
“Precision Medicine in the Age of ‘Big Data’: Leveraging Machine Learning and Genomics for Drug Discoveries”
Katie Gayvert, Weill Medical College (Cornell) and Geneseo math alumna, class of 2012.
Monday, April 17, 2:30, Newton 203.
Extra credit for a write-up.
Questions?
Functions on Sets
Why is it that if f : A → B is a function and C ⊆ A and D ⊆ A, f(C ∩ D) ⊆ f(C) ∩ f(D)? Find an example of sets C and D for which the subset is proper. Similarly find examples for C ⊆ f-1(f(C)) and f(f-1(E)) ⊆ E where E ⊆ B.
Consider an f that is not an injection, for instance f(1) = f(3) = b, f(2) = a, C={1,2}, D={2,3}. Then f(C ∩ D) = f({2}) = {a} but f(C) ∩ f(D) = f({1,2}) ∩ f({2,3}) = {b,a} ∩ {a,b} = {a,b}.
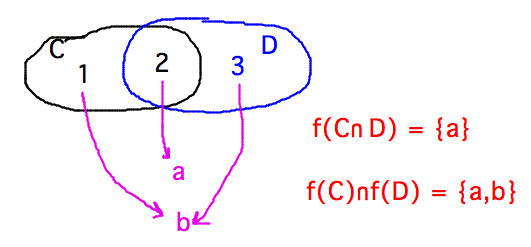
Concerning inverses, notice that f(C) = {b,a} but f-1( {b,a} ) = {1,2,3} because b has 2 preimages, so C ⊂ f-1( f(C) ).
You can similarly get a proper subset in f(f-1(E)) ⊂ E by considering a non-surjective f and including some values in E that aren’t images of anything under f.
Equivalence Relations
Textbook sections 7.1 and 7.2
Relations
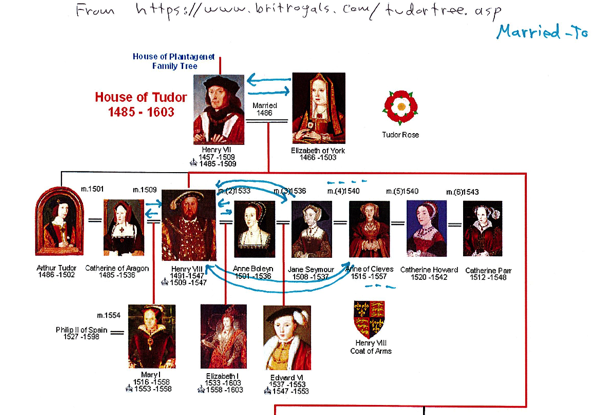
Describe as mathematical relations some of the family relations among the Tudors (see https://www.britroyals.com/tudortree.asp for the family tree).
Relevant ideas or questions from the reading:
- A relation is a collection (i.e., a set) of ordered pairs from 2 sets, e.g., pairs of the form (x,y) such that x∈A, y∈B form a relation from A to B.
- The domain of a relation is the set of all first coordinates (always elements of A).
- The range is the set of all second coordinates, always elements of B.
- You can graph relations, e.g., as regions in the coordinate plane or as vertices connected by edges.
Solutions:
- U = { Henry VII, Elizabeth of York, Arthur Tudor, ... }
- An Is-Parent-Of relation starts off Is-Parent-Of = { (Henry VII, Henry VIII), ... }
- Also a Married-To relation with the following partial graph (notice that this relation is symmetric, i.e., if a was married to b then b was married to a):
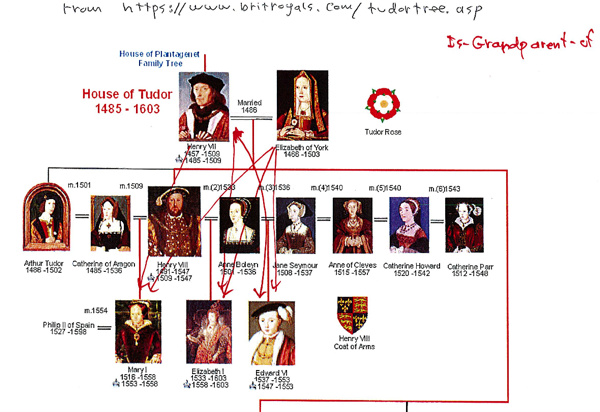
An Is-Grandparent-Of relation with this partial graph:
Comments:
- The most important thing here is simply what a relation is, i.e., the definition as a set of ordered pairs.
- It’s also good to understand the directed graph representation of relations.
Equivalence Relations
Are any of the relations you found so far equivalence relations? If not, find one.
Relevant ideas or questions from the reading:
- An equivalence relation has to be reflexive (everything is related to itself), symmetric (if a is related to b then b is related to a), and transitive (if a is related to b and b is related to c then a is related to c).
Solution: none of the relations so far is an equivalence relation. Married-To is closest because it’s symmetric, but it’s not reflexive or transitive.
Next
Equivalence relations and equivalence classes
- Try to find an equivalence relation in the Tudor family relations
Read textbook section 7.3