- In problem set 2 (and all later ones), you can use “theorems” from class or the book in your own proofs as long as either we have proved them in class, or the book has proved them, by the time you do the problem set
- Section 2.1
- Standard connectives are easy to implement electronically — how computers work
- Examples / problems
- Define Friday’s “nor” using “if and only if”
- P nor Q is true if and only if P is false and Q is false
- Example of biconditionals
- 7 > 3 iff it is 9:10 AM
- This is a legal biconditional statement that is false
- 7 > 3 implies 9:10 and 9:10 implies 7 > 3
- False and true = false
- Truth tables for Friday’s “nor” candidates?
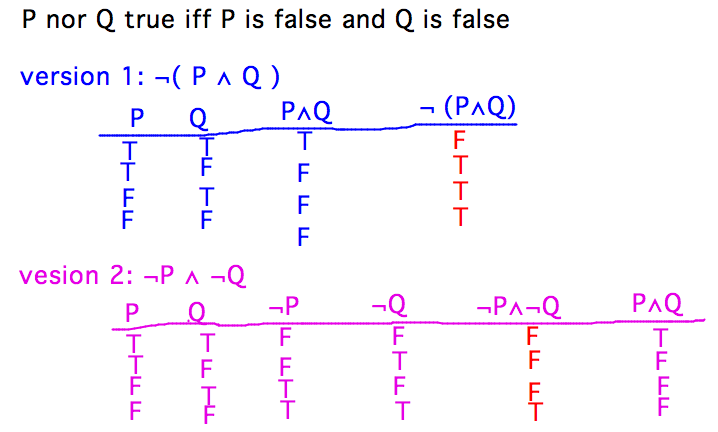
- Only version 2 captures the intended definition of nor
- Your own examples of tautologies and contradictions, especially in the real
world or everyday speech
- Tautology: P implies P
- Contradictions: P implies not P; you can have your cake and it eat too
- Define Friday’s “nor” using “if and only if”
- Equivalence of logical statements
- Read section 2.2