Purpose
This lesson develops your ability to use matrices and matrix operations in Matlab. In particular, it asks you to (1) create matrices representing simple geometric transformations, and (2) use matrix-vector arithmetic operations to apply those transformations to points. It also reinforces a couple of abilities introduced earlier in this course, including (3) your ability to program with functions, and (4) your ability to organize Matlab statements into scripts/functions/programs.
Background
We discussed matrices and matrix operations in class on February 17 and 20. Our textbook covers this material in chapter 8, with sections 8.1 and 8.3 being most directly relevant to this exercise.
This exercise asks you to use matrices to apply certain geometric transformations to plotted images. The key idea behind doing this is that if (x,y) is a point, then many geometric transformations can be generated by multiplying the column vector
x
y
by an appropriate matrix. We will look at examples in class. You can also get some insight into how these transformations work by applying them by hand to simple points.
For example, you can move the point to new coordinates (ax,by) by multiplying it by the matrix
a 0 0 b
If you multiply every point in some figure centered on (or otherwise referenced to) the origin by such a matrix, the effect is to make it a times bigger in the x dimension and b times bigger in the y dimension. For this reason, this transformation is called dilation or scaling.
You can also rotate a point counterclockwise around the origin through angle Θ by multiplying it by the matrix
cosΘ -sinΘ sinΘ cosΘ
Use a negative Θ to rotate clockwise. Once again, multiplying all points in a figure centered at the origin by such a matrix rotates the entire figure; if the figure isn’t centered at the origin the effect is as if the object was orbiting the origin.
Finally, you can do what is called shearing, which amounts to moving a point a distance in the x direction proportional to its y coordinate by multiplying by the matrix
1 k 0 1
where k determines how pronounced the shear is: a point will move k units in the x direction for every 1 unit in its y coordinate; k is typically less than 1.
Visually, shearing every point in an object makes it lean.
Activity
I have shared a “.m” file named “stickPerson.m” with you
via Canvas. To get the file in Canvas, either click here
or go to this course’s
“Files” tab and then to the “Lab Files” folder within it; you
should see “stickPerson.m” inside that folder. (If you can’t find it,
let me know and I will get it to you in some other way.) This file defines a function
named stickPerson that draws a stick figure person (who is named Stick
Person in the following discussion) when called, like so:
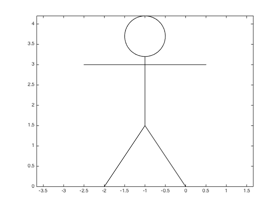
Your job is to do several things with this function, as follows:
Step 1
Modify the stickPerson function so that it takes one argument, namely
a matrix that describes a transformation of Stick Person. The modified function
should apply this transformation to every point in Stick Person before drawing
the person, so that what it actually draws is a transformed person. The pictures
below give some examples of transformed Stick Persons.
Test your modified function by calling it with a transformation that does nothing (i.e., an identity matrix) and verifying that it draws the figure shown above.
Step 2
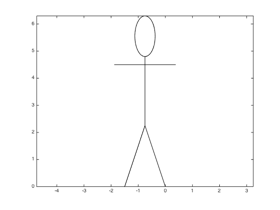
Write a script (or a section in a larger script) that calls your modified
stickPerson function with a transformation that makes it draw a tall
skinny Stick Person (this example is 1.5 times taller than normal and 0.75 times
as thick):
Step 3
Write a script (or a section) that calls your stickPerson function with
a transformation that makes it draw Stick Person leaning into the wind (or maybe
beckoning a Stick Person horde to follow somewhere):
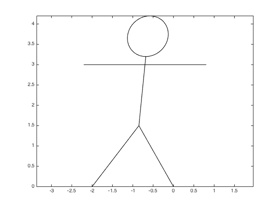
Once you have a matrix that makes Stick Person lean a certain amount, experiment with it and your program to try to figure out what transformations that matrix’s square, cube, and other powers produce.
Step 4
Finally, write a script (or a section) that uses your
stickPerson function to draw Stick Person doing a one-arm push-up:
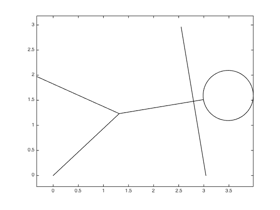
In writing this code, see if you can use Matlab to calculate how far you need to rotate Stick Person in order to get its right foot and right hand both on the ground (i.e., at y coordinate 0). It will help to know that the untransformed Stick Person’s right foot is on the origin, and that its right hand is at (0.5, 3).
Extras
If you have time after doing the above, there are lots of extra things you can do with this lab. For example, see if you can invent other interesting transformations of Stick Person. Try figuring out how you would apply several transformations at once, for example to draw the tall skinny Stick Person doing a push-up. Or just try making the basic Stick Person drawing look more sophisticated. Or use your imagination to invent other extensions…. Have fun!
Follow-Up
I will grade this exercise in a face-to-face meeting with you. During this meeting I will look at your solution, ask you any questions I have about it, answer questions you have, etc. Please bring your solution on your computer, as that will speed the process along.
Sign up for a meeting via Google calendar. Please make the meeting 15 minutes long, and schedule it to finish before the end of the “Grade By” date above.