Numerical Integration

Return to List of Lectures

Previous Lecture

Misc

I’m out of town next Friday (April 7). Class will be led by another math professor.

Questions?

Numerical Integration

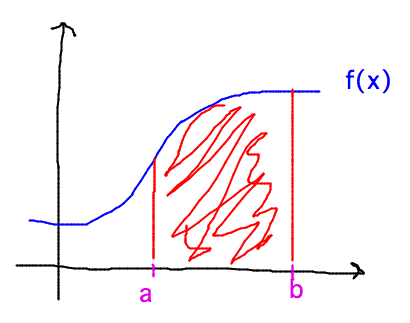
The basic idea is to evaluate a definite integral by numerically calculating the area under a curve:



Hand out lab

Goal for today: try some examples and develop pseudocode algorithms for numerical integration via Riemann sums and via the trapezoid rule.

For both methods, let’s use as an example function f(x) = x² - x, integrated from x = 1 to x = 4, with 3 subintervals.

Riemann Sums

Relevant ideas or questions from video

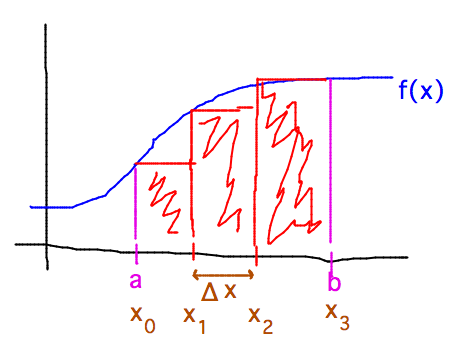
• Graph the function, then find rectangles under the graph
• i.e., divide the area under the curve into rectangular subregions
• Then the total area can be estimated via a formula based on the function values
  • In particular, the area of the subregion extending from x_i to x_i+1 is f(x_i) × ΔX
  • To get the total estimated area, you then add the areas of all the subregions



Try the example by hand

• ΔX = (4-1)/3 = 1
• x₀ = 1; f(x₀) = 0
• x₁ = 2; f(x₁) = 2
• x₂ = 3; f(x₂) = 6
• x₃ = 4; f(x₃) = 12
• Area = ΔX ( f(x₀)+ f(x₁)+ f(x₂) ) = 1 ( 0 + 2 + 6 ) = 8
  • Notice that this area calculation involved a small simplification: according to how we originally described the Riemann sum idea, the calculation should have been f(x₀)ΔX + f(x₁)ΔX + f(x₂)ΔX, but since ΔX is the same in all products, we could factor it out.
  • Also notice that we are calculating a left Riemann sum.

Algorithm

riemann( f, a, b, n )
    deltaX = ( b - a ) / n
    for each i between 0 and n
        xi = a + i * deltaX
        fi = f( xi )
    return (sum of f0 through fn-1) * deltaX    # left Riemann sum

Trapezoid Rule

Try to work through the example, and write out an algorithm, on your own. The algorithm should look about like the one for Riemann sums, except that it will calculate the area of each subregion differently.

Next

A new kind of loop: for loops

Read textbook section 12.4

Next Lecture