SUNY Geneseo Department of Mathematics
Monday, March 20
Math 230 02
Spring 2017
Prof. Doug Baldwin
CIT is looking to hire two student web assistants for fall 2017 and maybe beyond.
Mid-semester evaluation: short optional survey to tell me how this course is working for you and what you would or wouldn’t change.
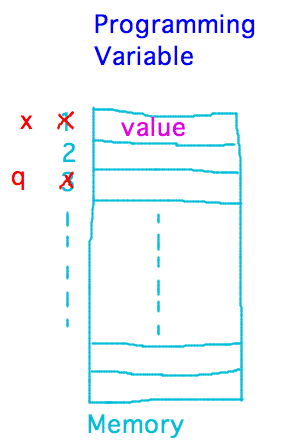
Example from before break: given 2 positive integers, x and y, find the number of times y goes into x (q), along with the remainder (r) of that division. Use a while loop to count how many times you can subtract y from x.
Notice that at the end, x = qy + r. Furthermore, r will be between 0 and y-1, i.e., 0 ≤ r < y. So you could start by giving q and r values that trivially satisfy x = qy + r and then use a while loop to refine them into values that also satisfy 0 ≤ r < y.
The idea for “refining” q and r is to subtract y from r to bring it closer to the desired 0 ≤ r < y range, but each time we do that subtraction we have to add 1 to q to maintain the relation x = qy + r.
function [ q, r ] = quotientAndRemainder( x, y )
%QUOTEINTANDREMAINDER Compute the integer quotient of x divided by y and
% the remainder, for positive integers x and y.
% x = qy + r
% 0 <= r < y at end
q = 0;
r = x;
while ( r >= y )
% Refine q and r until 0 <= r < y and x still equals qy + r
r = r - y
q = q + 1
end
endRunning this produces results such as this (including the intermediate values of q and r since I didn’t suppress their output)
>> [q,r] = quotientAndRemainder( 19, 5 )
r =
14
q =
1
r =
9
q =
2
r =
4
q =
3
q =
3
r =
4You’ve now seen pretty much everything you can do with variables in programming, and it’s not the same as what you can do with variables in math.
What are the differences? For example...
>> % Try to solve x + y = 2 and x - y = 0
>> x + y = 2; x - y = 0
x + y = 2; x - y = 0
↑
Error: The expression to the left of the equals sign is not a valid
target for an assignment.Why do these differences exist?

Algorithms. Watch this video on the concept of algorithm if you haven’t already.
More about while loops.