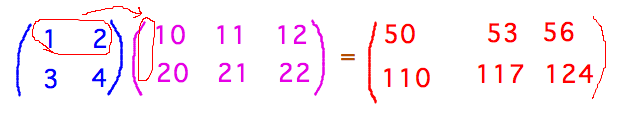Introduction to Matrices

Return to List of Lectures

Previous Lecture

Misc

Appointments with me can be for anything, not just grading.

Questions?

Matrices

Sections 8.1 - 8.3

Example. Compare individual guesses about how many legos of various colors are in each of 3 bags to the average of the guesses.

Everyone make a matrix of your guesses by color and bag:

	Bag 1	Bag 2	Bag 3
Gray
Green
Black

Then gather several tables and calculate an average table.

Reading ideas

• Create 2D arrays using semicolons and brackets
• Access elements with arrayname( row, column )
• The row and column integers are called “indices”
• Linear indexing can access an element with just 1 index
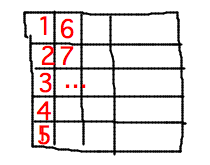
  • Formula for linear index of row r column c in an m-row by n-column array is (c-1)m + r
  • Linear indexing counts down consecutive columns



• You can use out-of-range indices to resize an array by assigning a value to an out-of-range element, but out-of-range indexing is an error if you try to read the element at that index
• You can do arithmetic between matrices as long as those matrices have the same number of rows and columns (or a compatible number for matrix multiplication).

Here is some code for creating and averaging matrices, as well as picking an element out with indexing:

>> P = [ 4,5,6 ; 5,6,6 ; 4,5,4 ]
P =
     4     5     6
     5     6     6
     4     5     4
>> G = [ 5,4,8; 4,3,4; 6,9,2 ]
G =
     5     4     8
     4     3     4
     6     9     2
>> E = [ [ 1 2 3]; ...
[ 3,4,5]; ...
[ 5,6,7] ]
E =
     1     2     3
     3     4     5
     5     6     7
>> Avg = (P+G+E) ./ 3
Avg =
    3.3333    3.6667    5.6667
    4.0000    4.3333    5.0000
    5.0000    6.6667    4.3333
>> Avg( 3, 1 )
ans =
     5

There are other ways to create matrices, too, as demonstrated here:

>> zeros( 7, 9 )
ans =
     0     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0     0
>> ones( 7, 9 )
ans =
     1     1     1     1     1     1     1     1     1
     1     1     1     1     1     1     1     1     1
     1     1     1     1     1     1     1     1     1
     1     1     1     1     1     1     1     1     1
     1     1     1     1     1     1     1     1     1
     1     1     1     1     1     1     1     1     1
     1     1     1     1     1     1     1     1     1
>> eye( 8 )
ans =
     1     0     0     0     0     0     0     0
     0     1     0     0     0     0     0     0
     0     0     1     0     0     0     0     0
     0     0     0     1     0     0     0     0
     0     0     0     0     1     0     0     0
     0     0     0     0     0     1     0     0
     0     0     0     0     0     0     1     0
     0     0     0     0     0     0     0     1
>> rand( 4, 8 )
ans =
  Columns 1 through 7
    0.8147    0.6324    0.9575    0.9572    0.4218    0.6557    0.6787
    0.9058    0.0975    0.9649    0.4854    0.9157    0.0357    0.7577
    0.1270    0.2785    0.1576    0.8003    0.7922    0.8491    0.7431
    0.9134    0.5469    0.9706    0.1419    0.9595    0.9340    0.3922
  Column 8
    0.6555
    0.1712
    0.7060
    0.0318

Example. Book’s Challenge Activity 8.2.1 (index and return the middle element of an n-by-n array).

Well worth looking at, but it won’t fit on the small projector in the classroom for group work.

What Is Matrix Multiplication? A multiplication rule that associates each element of each row of the first matrix with a row of the second matrix, and multiplies them. You then add the results to get the row in the product corresponding to whichever row of the first matrix you used.



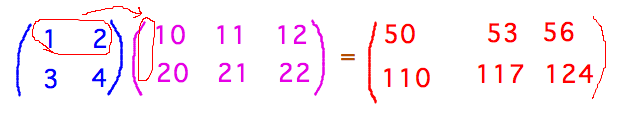
Next

Geometric transformations as matrix multiplication

And a new lab

But no new reading

Next Lecture