Lesson 7—Finding Zeros with Newton’s Method

Purpose

This lesson introduces you to Newton’s method, an important algorithm for finding zeros of functions, as well as to several other mathematical programming tricks. It also introduces a new Matlab statement, the if statement, and reinforces your understanding of while loops.

Background

Given a function, f(x), a zero of f is simply a value of x at which f(x) = 0. Finding zeros of functions is the heart of algorithms for solving many mathematical problems, as illustrated later in this exercise.

Newton’s method, sometimes called the Newton-Raphson method, is a simple and widely used algorithm for finding zeros. For a description of it and the underlying mathematics, see the video lecture entitled “Newton-Raphson Method: Derivation” at https://www.youtube.com/watch?annotation_id=annotation_134081&feature=iv&src_vid=lFYzdOemDj8&v=nRbsfnUftT4.

Sections 4.1 through 4.3 of Attaway’s text discuss if statements. You can also find a video lecture on it at http://www.see.ed.ac.uk/teaching/courses/matlab/unit04/if-else-statement.shtml.

Activity

The basic plan for this exercise is to write a Matlab function that uses Newton’s method to find a zero of a given function, write a supporting function that calculates derivatives, and finally use the Newton’s method function to solve several problems that reduce to zero-finding. Here are the details…

Step 1

Write a function, which I’ll call derivative in this handout, that takes a function handle, f, and a number, x, as its arguments, and that returns a close approximation to the derivative of f evaluated at x. For an alternative version of this task, see the extra credit section below.

We will develop an algorithm for approximating derivatives of arbitrary functions through class discussion.

Step 2

Write a function, newton, that takes a function handle, f, and a number, x, as its parameters, and that returns a close approximation to a zero of f. Your function should use Newton’s method, with x as its initial estimate of the zero, to find its answer. Your function should also use the derivative function from step 1 to calculate the derivatives that Newton’s method uses.

Step 3

Use the newton function from step 2 to solve the following problems. It may be helpful to write a script for each problem, possibly broken into sections that you can execute individually (via the “Run Section” button in Matlab’s editor), to organize the code you use in solving each problem. We will develop algorithms for these problems through class discussion if needed.

Problem 1. Find a solution to the equation

cosx = -2x

Problem 2. Given a positive number, x, calculate √x, without using any explicit root or exponentiation operations. (Needing to do this is a situation that the designers of the “square root” functions in calculators and programming languages face—they can’t use a built-in operation because they are the ones building the operation in to begin with! Wisdom has it that many calculators, computers, and programming languages do in fact use Newton’s method to implement their square root (and certain other) operations.)

Problem 3. Find the zeros of a function defined piecewise as follows:

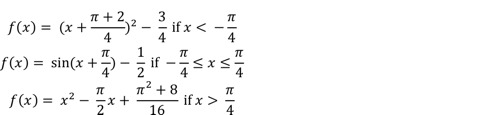
Hint: you might find it helpful to plot this function in order to get a rough sense of where its zero(s) is/are, then use Newton’s method to home in on the zero(s).

Extra Credit

For up to 2 points extra credit, write the derivative function so that it only takes the function handle, f, as its parameter, and returns a new handle to a function that is (a close approximation to) the derivative of f. Note: this does not require you to write or use any symbolic differentiation code.

Follow-Up

I will grade this exercise in a face-to-face meeting with you. During this meeting I will look at your solution, ask you any questions I have about it, answer questions you have, etc. Please bring a written solution to the exercise to your meeting, as that will speed the process along.

Sign up for a meeting via Google calendar. If you worked in a group on this exercise, the whole group should schedule a single meeting with me. Please make the meeting 15 minutes long, and schedule it to finish before the end of the “Grade By” date above.