Problem Set 2 — 3-Dimensional Surfaces

Purpose

This exercise reinforces your understanding of common surfaces in 3-dimensional space, including their plots. The exercise also gives you some practice working with cylindrical coordinates. It therefore contributes to the following learning outcomes for this course:

• Outcome 1. Represent vectors analytically and geometrically, and perform vector calculations
• Outcome 12. Use technological tools such as computer algebra systems or graphing calculators for visualization and calculation of multivariable calculus concepts.

Background

This exercise is based on material in sections 1.6 and 1.7 of our textbook. We discussed this material in classes between January 31 and February 3. This exercise also asks you to plot surfaces with Mathematica. I introduced that in class on January 30, with examples continuing through the classes since.

Activity

Solve each of the following problems.

Problem 1

For each of the following equations, try to determine what sort of quadric surface it describes before plotting that surface, including any details you can about what axis (if any) the surface aligns with, where its center is, etc. Then plot the surface with Mathematica to check your ideas.

(Note: I will want to see your Mathematica work when we meet to grade this problem set. There’s no way I can tell whether you really did it after rather than before deciding what sort of surface you were looking at, and I won’t try to. But I probably will ask you to solve a similar problem during grading, when obviously I can see that you’re deducing things about the surface before you look at the plot, so getting the practice while working on this problem will be helpful.)

1. \(z = \frac{x^2}{9} - \frac{y^2}{4}\)
2. \(y^2 + z^2 - x^2 = 4\)

Problem 2

Think about the spheres \(x^2 + y^2 + z^2 = 4\) and \((x-4)^2 + y^2 + z^2 = 9\). These spheres intersect, and this exercise guides you through finding an equation that describes their intersection. (Note that spheres such as this are hollow, i.e., points inside them do not satisfy the given equations. Thus the intersection is the curve where the surfaces of the spheres meet, not a solid shape.)

Step A

Use Mathematica to plot the two spheres on a single set of axes, and confirm visually that they do indeed intersect. Based on the plot, what shape do you expect the intersection to have?

Step B

Since both spheres are centered on the \(x\) axis, there is a single \(x\) value for all the points in their intersection. Calculate what this value is. (Hint: this is probably the hardest part of the question. One way to go about it is to see if you can solve for a value of \(x\) that makes both the equations \(x^2 + y^2 + z^2 = 4\) and \((x-4)^2 + y^2 + z^2 = 9\) hold. I can also answer questions about this question in class if you ask.)

Part C

Once you have a value for \(x\), use it to find an implicit equation that relates the \(y\) and \(z\) values for points in the spheres’ intersection. Decide whether this equation describes the shape you expected from the plot in Part A.

Problem 3

Do you think it would be possible to have something analogous to cylindrical coordinates for 4 dimensional space? If so, describe (as well as you’re able) how the coordinates could work. If not, describe (again, as well as you’re able) why not. (Hint: I think there are multiple correct answers to this question; you only need to come up with one, but if you talk to others about it you might find that the group has several different answers, and they could all be good ones.)

Problem 4

Our textbook gives some examples of equations or systems of equations that describe certain planes, lines, etc. in spherical and cylindrical coordinates. The problems in this question are similar, except they use inequalities to define regions.

Part A

What shape (e.g., a square, a triangle, etc.) is the region described by the cylindrical equations and inequalities…

• \(\Theta = \frac{\pi}{4}\)
• \(0 \le r \le 1\)
• \(0 \le z \le r\)

Part B

Using equalities and/or inequalities, somewhat as in Part A, describe the shape of a wedge-shaped slice cut from a piece of cake, sort of like this:

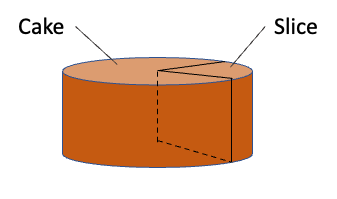
Assume that the origin of the coordinate system is at the center of the bottom of the cake, with the \(z\) axis running vertically up through its center. Also assume that the angle at the apex of the slice is \(\frac{\pi}{6}\) radians, or \(30\) degrees, the radius of the cake is 4 inches, and its height is 5 inches. You may position the slice anywhere you like around the cake.

Follow-Up

I will grade this exercise during an individual meeting with you. That meeting should happen on or before the “Grade By” date above, and should ordinarily last half an hour. During the meeting I will look at your solution, ask you any questions I have about it, answer questions you have, etc. Sign up for the meeting via Google calendar. Please have a written solution to the exercise ready to share with me during your meeting, as that will speed the process along.