SUNY Geneseo Department of Mathematics

Problem Set 11 — Multivariable Integrals

Math 223
Spring 2023
Prof. Doug Baldwin

Complete by Friday, April 21
Grade by Friday, April 28

Purpose

This exercise develops your understanding of integration in multiple dimensions. It therefore contributes to the following learning outcomes for this course:

Outcome 7. Evaluate double and triple integrals
Outcome 8. Use multiple integrals to find area and volume
Outcome 12. Use technological tools such as computer algebra systems or graphing calculators for visualization and calculation of multivariable calculus concepts.

Background

This exercise is mainly based on material in sections 4.1 through 4.4 of our textbook. We covered that material in classes between April 7 and 14. This problem set also asks you to evaluate multiple integrals with Mathematica. We saw some examples of that in class on April 14.

Activity

Solve each of the following problems.

Problem 1

Let region $D$ be the region between the curves $y = x^{2} - 4$ and $y = 4 - x^{2}$ , illustrated here:

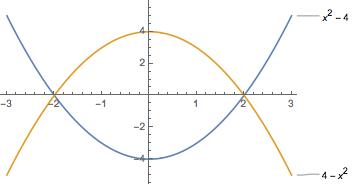
Region bounded between a parabola and its negative, intersecting on the X axis at X equals negative 2 and X equals 2, and reaching extremes of 4 and negative 4 on the Y axis

Part A

Evaluate

\iint_{D} (x^{2} + y) d A

over region $D$ . Check your answer by also evaluating the integral with Mathematica.

Part B

Use a double integral to find the area of region $D$ . Check your answer by also evaluating the integral with Mathematica.

Problem 2

One of the properties of double integrals that our textbook states is that over a rectangular region $R = [a, b] \times [c, d]$

\iint_{R} g (x) h (y) d A = (\int_{a}^{b} g (x) d x) (\int_{c}^{d} h (y) d y)

Justify this claim by showing how to express the double integral from the left side of the equation as an iterated integral and then rearrange it into the product on the right side.

Problem 3

Evaluate

\int_{0}^{3} \int_{0}^{2} \int_{0}^{1} \int_{0}^{z} d w d z d y d x

Give an interpretation of this integral as a “volume” (or, technically, hypervolume) that helps you make sense of the value you calculated.

Problem 4

(Based on Exercise 11 in section 4.2E of our textbook.)

Evaluate

\iint_{D} x y d A

Where $D$ is the region $- 1 \leq y \leq 1$ , $y^{2} - 1 \leq x \leq \sqrt{1 - y^{2}}$ .

Check your result by also evaluating the integral with Mathematica.

(Hint: this is an ugly-looking integral that turns out to have a simple result if you simplify it right.)

Follow-Up

I will grade this exercise during an individual meeting with you. That meeting should happen on or before the “Grade By” date above, and should ordinarily last half an hour. During the meeting I will look at your solution, ask you any questions I have about it, answer questions you have, etc. Sign up for the meeting via Google calendar. Please have a written solution to the exercise ready to share with me during your meeting, as that will speed the process along.