SUNY Geneseo Department of Mathematics
Friday, January 24
Math 223 01
Spring 2020
Prof. Doug Baldwin
Correction to final exam date: it’s actually Friday, May 8 (still at noon).
Does the strategy for finding an equation for a plane extend to lines? Yes, for a line parallel to a certain axis you would give a system of equations that say the other 2 variables are equal to appropriate constants, e.g., x = 10, y = -2.
What do you call a slice of a 4- or higher-dimensional space? A “hyperplane,” at least if it’s a “flat” slice.
Can you also have equations for other shapes besides the ones shown in the text, e.g., pyramids? Yes, although in some cases (like pyramids) it might actually be a set of equations that describe the individual sides of the shape.
First part of section 11.2
The idea of 3D coordinates.
The distance formula in 3 dimensions, and other formulas such as the midpoint formula extended from 2 dimensions to more.
Equations for spheres, cylinders, planes, (and now lines thanks to the question you asked).
For future: the definition of a vector in space.
Relative to the coordinate system in the classroom, where is point (2,1,-2)? As we had the coordinate system set up, (2,1,-2) was towards the front of the room on the floor.
What are the coordinates of a certain cupholder in the classroom? About (1,4,-1).
What can you say about what a 4-dimensional coordinate system would be? It would have 4 axes, all perpendicular to each other, and they would intersect at a single point (the origin). (In coming up with this answer, you did quite a bit of identifying the important abstract ideas of “coordinate system” - axes, perpendicularity, origin - from the two concrete examples you’ve seen. Congratulations!)
Can you figure out the distance from (3,2,4,0) to (5,1,2,-3)?
Just as the distance formula in 2 dimensions extended to 3, it extends similarly to more. Here we assumed 4-dimensional points are of the form (w,x,y,z):
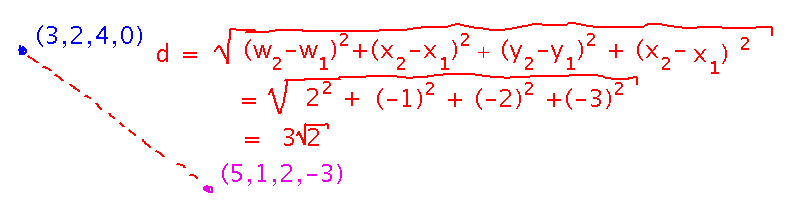
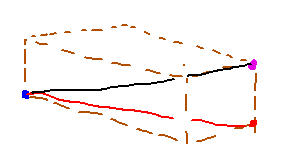
The reason for this is that you can calculate distances in 3 or more dimensions as a series of calculations of distances in planes:
Similar to example 11.2.3...
Give an equation for the plane containing (1,2,3) and parallel to the xy plane.
z = 3
Can you find a system of equations defining a line through (1,2,3) and parallel to the y axis?
x =1, z = 3
How about equation(s) for a plane through (1,2,3,4) parallel to the xz plane? (Call the 4th dimension w if you need a variable for it.)
Assuming points are (x,y,z,w): y = 2, w = 4
(The (x,y,z,w) order is probably more common than the (w,x,y,z) one we used in an earlier example.)
Introduction to Mathematica for plotting and otherwise working with equations and surfaces in space.
Assignment for Monday: get Mathematica installed on your computer. See the CIT helpdesk (now in Sturges) or me if you run into any trouble.
Bring your computer to class Monday.