- Sign up for problem set 10 appointments
- Section 16.3
- Confusing, connections between pieces?
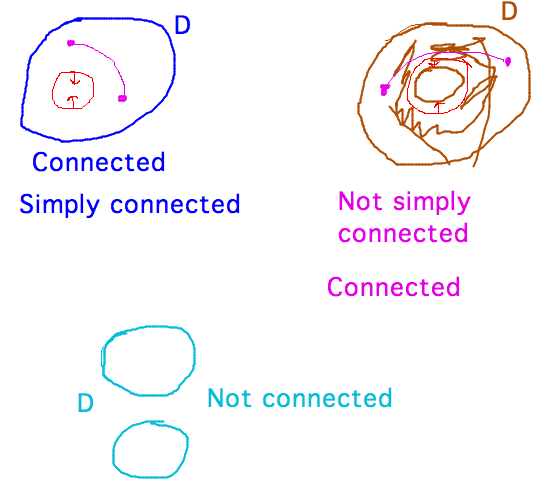
- Connected, simply connected domains?
- Intuitively, connected means you can draw a possibly curved line between any 2 points in the set without leaving the set
- Simply connected means any circle in the set can be pulled tight into a point
without leaving the set
- Path independence ?
- You saw an example when we integrated work over 2 flights of stairs that reached the same height—the integrals were the same, independent of the path of the stairs
- Integral of F same over all paths
- Equivalent to field being conservative
- F is field = gradient of f ?
- Main new thing here is name “potential function,” a label that’s useful for talking about integrals of conservative fields
- f is potential function for F
- Fundamental theorem of line integrals

- Conservative fields are gradient fields ?
- This basically just states a useful connection between 2 kinds of vector fields
- Closed loop integral = 0 iff field conservative ?
- That the integral is 0 follows from the fundamental theorem

- But other direction also interesting, i.e., if you find that integrals around closed loops are always 0 then you know your field is conservative
- That the integral is 0 follows from the fundamental theorem
- Component test for conservative fields ?

- Unintuitive now, but we may be able to see where this comes from in a week or so
- Exact differential forms ?
- M(x,y,z) dx + N(x,y,z) dy + P(x,y,z) dz
- Exactness captures the differential form of those line integrals that happen to be of vector fields
- Examples
- Let f(x,y,z) = x(y-sin(z2)) / (z2 + exy), let
F = grad f, and let C be the curve x = sint cost, y = t2(π/2-t),
z = π, 0 ≤ t ≤ π/2
- Find the integral of F around C

- 0, by closed loop theorem and because F is conservative—it’s a gradient field
- Find the integral of F from ( 0, 0, 0 ) to ( 1, 0, √(π/2) )
- By fundamental theorem, integral = f(1, 0, √(π/2) ) - f( 0, 0, 0 )
- = 1 ( 0-sin(π/2) ) / ( π/2 + e0) - f(0,0,0) = -1 / (π/2 + 1) - 0
- Find the integral of F around C
- Is F(x,y,z) = ⟨ x+y, y+z, z+x ⟩ conservative?
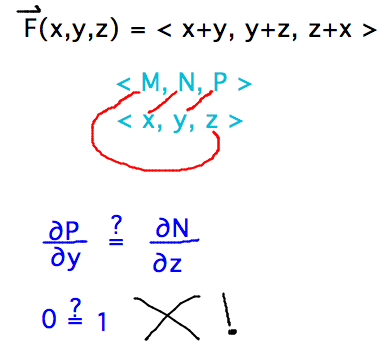
- How about ⟨ x2, y2, z2 ⟩?
- Component test says it is
- So also find potential function
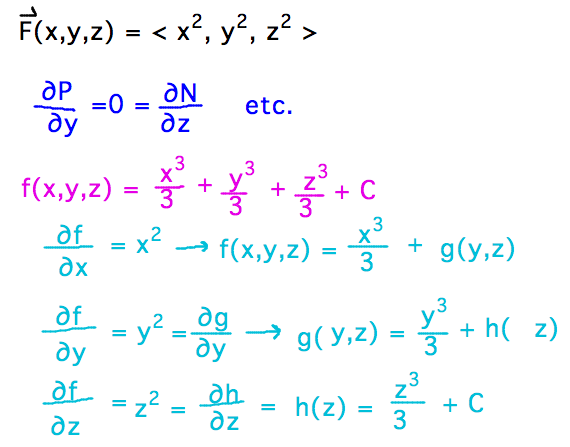
- Potential function for F(x,y,z) = ⟨ cosx siny, sinx cosy + z, y + 2
⟩
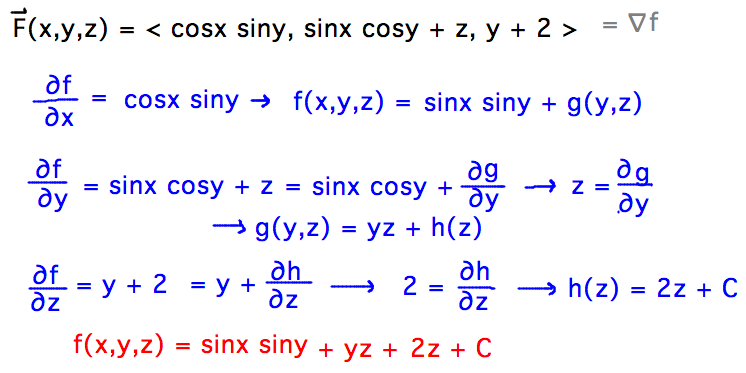
- Let f(x,y,z) = x(y-sin(z2)) / (z2 + exy), let
F = grad f, and let C be the curve x = sint cost, y = t2(π/2-t),
z = π, 0 ≤ t ≤ π/2
- Problem set
- Green’s Theorem
- Read section 16.4