- GREAT Day
- (Day of student research talks, art exhibits/performances, etc.)
- Tuesday, April 19
- No class(es)
- Extra credit (up to 2 problem set points per summary) for math session summaries
- 1 paragraph to 1 page discussing whatever connects the presentations in a session to each other
- At most 3 sessions per person for extra credit
- 3rd and 4th parts of section 16.2
- Tangent vector to parameterized path points “forward”
- Line integral is integral of tangential component of field along curve

- To evaluate:
- Parameterize path
- Plug parametric versions of x, y, z into field function
- Integrate
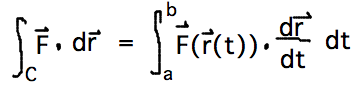
- Line integrals wrt dx, dy, dz
- Can define vector with only 1 component in order to integrate wrt that variable

- Can define vector with only 1 component in order to integrate wrt that variable
- Arc length as a line integral

- Questions
- Are these and Tuesday’s scalar line integrals really the same thing?
- Yes

- Yes
- How come vector field line integrals and integrals such as M(x,y,z) dx even get to
be the same chapter?
- Book formula for sum of integrals of M dx, N dy, and P dz is really just the integral of the dot product of F with derivative of r
- So F dot dr and M dx + N dy + P dz are really just different notations for the same line integral
- Are these and Tuesday’s scalar line integrals really the same thing?
- Examples
- F(x,y,z) = ⟨ y, -x, z ⟩, C: straight line from (-1,-1,-1) to (1,1,1)
- Field spirals away from XY plane

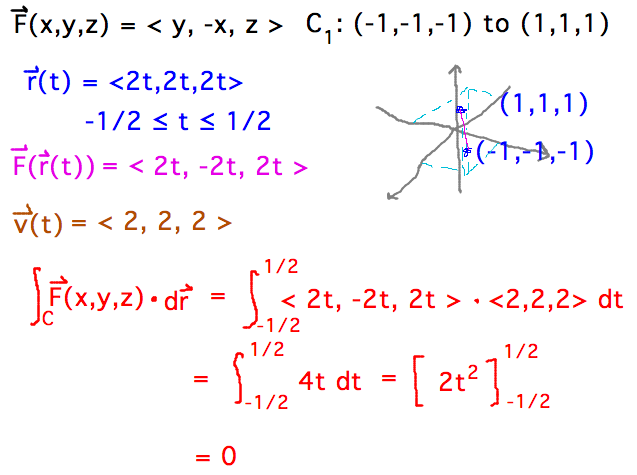
- Field spirals away from XY plane
- Integrate force of gravity (= ⟨0,0,-w⟩ where w is your weight) over
spiral (r(t) = ⟨ 2cos(2πt), 2sin(2πt), 10t ⟩) and zigzag
( r1(t) = ⟨0,10t,5t⟩, r2(t) =
⟨0,10-10t,5+5t⟩ ) staircases from Tuesday
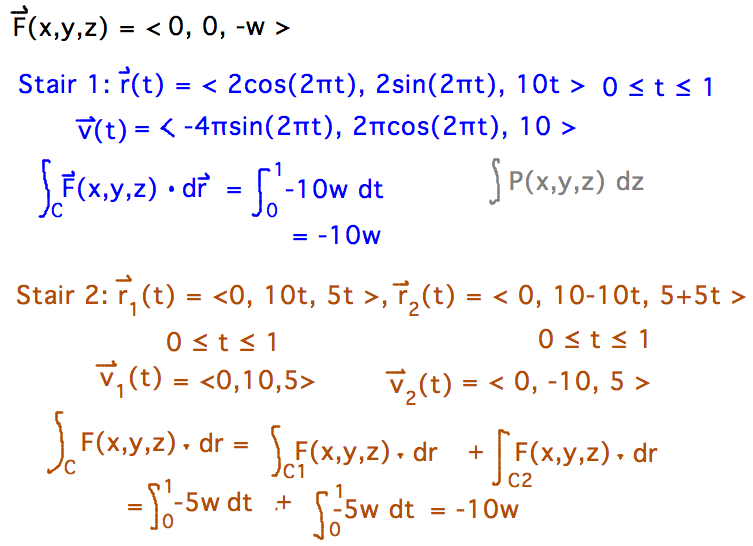
- F(x,y,z) = ⟨ y, -x, z ⟩, C: straight line from (-1,-1,-1) to (1,1,1)
- Applications of line integrals of vector fields
- Read rest of section 16.2