- Section 14.7
- Local minimum, maximum
- Saddle point: in every disk around P0 some points have f(x,y) < f(P0) and some have f(x,y) > f(P0)
- Critical points: fx = fy = 0, or derivatives don’t
exist
- Extrema can exist here
- 2nd derivative test for local extrema
- To find absolute minima, maxima on closed bounded regions
- List interior points that might be extrema
- List boundary points that might be extrema
- Find most extreme items in both lists
- Examples
- z = x2 + y2

- z = x3/3 - x2 + y2 + 2y

- Plot this to see what it looks like in detail
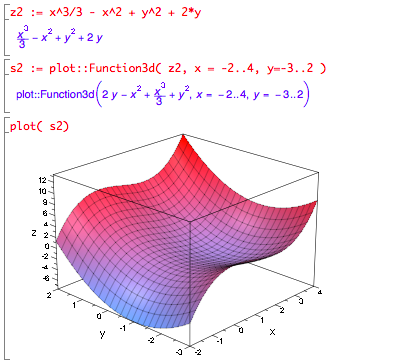
- Plot this to see what it looks like in detail
- z = x3y3
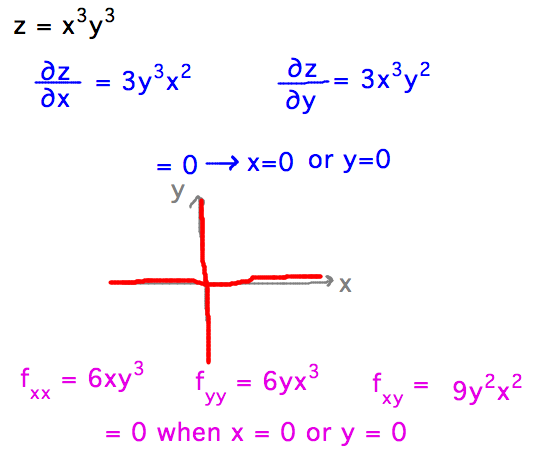
- This function has infinitely many critical points, and they’re all saddle
points, though you have to use the definition of saddle point to realize that
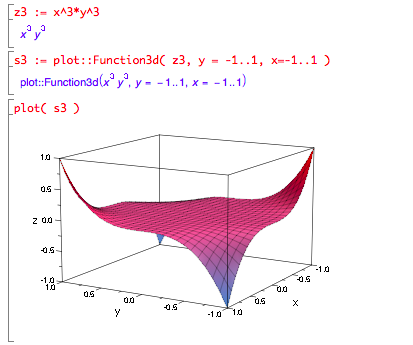
- This function has infinitely many critical points, and they’re all saddle
points, though you have to use the definition of saddle point to realize that
- z = x2 + y2
- Problem set
- Absolute maxima and minima
- No reading