- PRISM Mentoring
- Wednesday, March 9, 3:30
- South 328
- Advice from math majors re course selection, summer experiences, etc.
- Gives general ideas if not concrete details for solving each problem.
- See https://docs.google.com/document/d/1jNb-mOjDSHtkqmQveOhjwm1pzfXct8q2zIyDmKrMiK4/edit
- Comments, feedback, etc. welcome
- Curvature of parabola question?
- Could do direct calculation of k
- Or use formula for curvature of twice-differentiable function in exercise 5a
- lim(x,y)→(0,0)( 3x3 / (x3+y) )
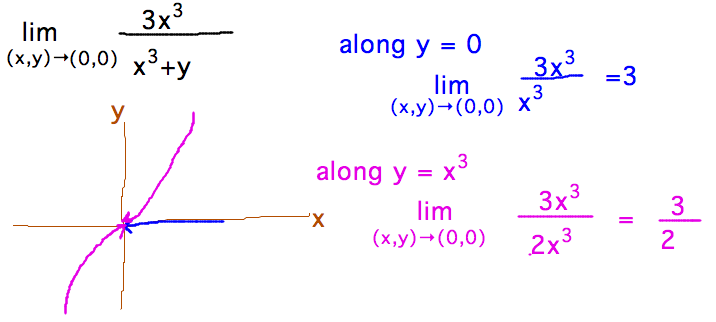
- Section 14.3
- Definition of partial derivative

- Notations
- Can apply to functions with more than 2 variables
- Treat all variables other than one you differentitate with respect to as constants
- e.g., in ∂f(x,y)/∂x treat y as constant
- Function can have partial derivatives without being continuous
- 2nd order partial derivatives are derivatives of derivatives
- Notations
- ∂2f/∂x2 or fxx
- Similar for other variables
- ∂2f/(∂x∂y) differentiates wrt y first also fyx
- Notations
- Mixed derivative theorem?
- For suitably continuous functions, order of differentiation for second derivatives doesn’t matter
- ∂f/(∂x∂y) = ∂f/(∂y∂x)
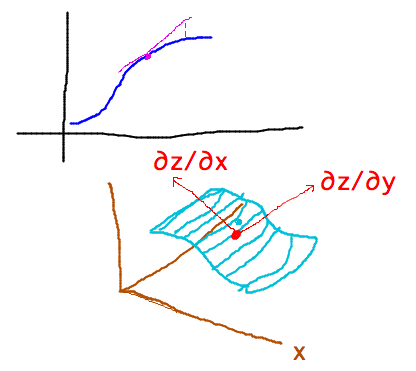
- Increment theorem?
- For a function with continuous derivatives, the change in a function’s
value near (x0,y0) is the change in x and/or y times the
corresponding derivative plus a correction factor that diminishes with
diminishing change in x, y
- For a function with continuous derivatives, the change in a function’s
value near (x0,y0) is the change in x and/or y times the
corresponding derivative plus a correction factor that diminishes with
diminishing change in x, y
- Differentiability implies continuity?
- Definition of “differentiable” says function satisfies increment theorem
- This requires more than just that the partial derivatives exist
- Definition of partial derivative
- Examples
- Find first partial derivatives of z = xy2 - y sinx
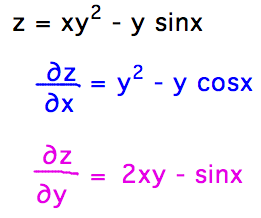
- Find slopes of auditorium function (z = √( 400 - (x-y)2/2 ) ) in
x and y directions at (x,y) = (0,10)

- Derivative with respect to y is similar, except with opposite sign
- Slope in y direction is thus just the negative of slope in x direction
- Find first partial derivatives of z = xy2 - y sinx
- The chain rule for partial derivatives
- Read section 14.4