- Rochester Math Olympiad
- Western NY regional math problem-solving contest
- 4 problems in 3 hours
- Small cash prizes for top 3 finishers in region
- Feb. 6 (this Saturday), 9:30 - 12:30
- See Prof. Towsley to join
- Section 12.3
- Define dot product
- ⟨u1,u2,u3⟩ ⋅ ⟨v1,v2,v3⟩ = u1v1 + u2v2 + u3v3
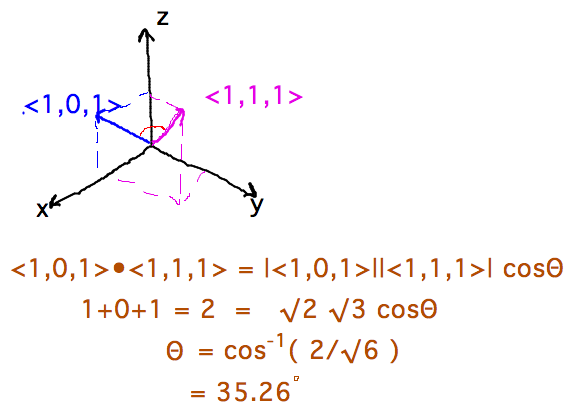
- a = cos-1 ( u⋅v / |u||v| ) where a is angle between vectors
- Finds component of 1 vector in direction of other
- Perpendicular or orthogonal vectors have dot product 0 (cos(90°) = 0)
- Properties
- u⋅v = v⋅u
- cu ⋅ v = c (u⋅v)
- u⋅(v+w) = u⋅v + u⋅w
- u⋅u = |u|2
- 0⋅u = 0
- Projection: projvu = cos(a) |u| v/|v|
- Represents component of u parallel to v
- Scalar component of u in direction v = magnitude of projvu
- e.g., force from u in direction v
- Work = force over a distance
- Calculated from dot product if force not in direction of displacement
- Define dot product
- Examples
- ⟨ 1, 2, 3 ⟩ ⋅ ⟨ 3, -2, 3 ⟩ = 1×3 + 2×(-2) + 3×3 = 8
- ⟨ 4, -2 ⟩ ⋅ ⟨ 1, 3 ⟩ = 4×1 + (-2)×3 = -2
- ⟨ 2, 4, 3, 2 ⟩ ⋅ ⟨ 1, 5, -1, 2 ⟩ = 2×1 + 4×5 + 3×(-1) + 2×2 = 23
- Suppose v = ⟨ x, y, z ⟩. How to use dot product to pick out component in i, j, or k direction?
- For example, ⟨x,y,z⟩ ⋅ ⟨0,1,0⟩ = y
- More generally, ⟨x,y,z⟩ ⋅ i, j, or k, is component in i, j, or k direction, respectively
- Show that if v = ⟨ a, b, c ⟩, then the vector u =
⟨ b-c, c-a, a-b ⟩ is orthogonal to v
- v ⋅ u = ab - ac + bc - ba + ca - cb = 0 by cancellation
- Note that “orthogonal” and “perpendicular”
don’t mean exactly the same thing

- Find angle between ⟨1,0,1⟩ and ⟨1,1,1⟩
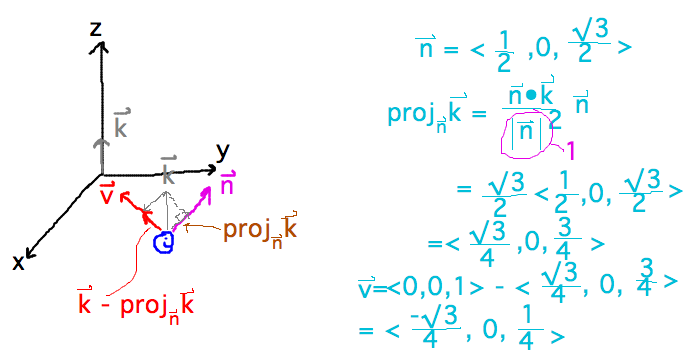
- Projections and computer games/graphics
- Given direction (i.e., vector) viewer is looking in, need to derive a vector pointing
in viewer’s “up” direction as part of coordinate system relative to
which viewer actually sees things
- Given direction (i.e., vector) viewer is looking in, need to derive a vector pointing
in viewer’s “up” direction as part of coordinate system relative to
which viewer actually sees things
- Cross product
- Read section 12.4