SUNY Geneseo Department of Mathematics

Problem Set 10 — Integrals

Math 223 01
Fall 2022
Prof. Doug Baldwin

Complete by Sunday, November 13
Grade by Friday, November 18

Purpose

This exercise reinforces your understanding of definite integrals of multivariable functions. It contributes to the following learning outcomes for this course:

Outcome 7. Evaluate double and triple integrals
Outcome 8. Use multiple integrals to find area and volume
Outcome 12. Use technological tools such as computer algebra systems or graphing calculators for visualization and calculation of multivariable calculus concepts.

Background

This exercise is based on material in sections 4.1 through 4.4 in our textbook. We covered those sections in classes between October 31 and November 4.

The problem set also asks you to use Mathematica to evaluate integrals. We discussed how to do this in class on November 4.

Activity

Solve each of the following problems.

Problem 1

Evaluate

\int_{0}^{1} \int_{1}^{2} \int_{0}^{2} x^{2} y^{2} z^{2} d z d y d x

Check your answer by also evaluating the integral with Mathematica.

Problem 2

Let region $D$ be the region between the curves $y = x^{2} - 4$ and $y = 4 - x^{2}$ , illustrated here:

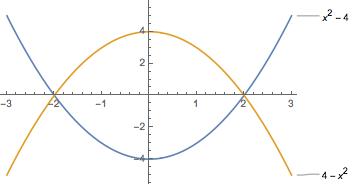
Region bounded between a parabola and its negative, intersecting on the X axis at X equals negative 2 and X equals 2, and reaching extremes of 4 and negative 4 on the Y axis

Part A

Evaluate

\iint_{D} (x^{2} + y) d A

over region $D$ . Check your answer by also evaluating the integral with Mathematica.

Part B

Use a double integral to find the area of region $D$ . Check your answer by also evaluating the integral with Mathematica. (We haven’t done examples in class of exactly this sort of problem, but it is mentioned in the book, and we certainly can do an example in class if anyone would like.)

Part C

Find the average value of $x^{2} + y$ over region $D$ .

Problem 3

One of the properties of double integrals that our textbook states is that over a rectangular region $R = [a, b] \times [c, d]$

\iint_{R} g (x) h (y) d A = (\int_{a}^{b} g (x) d x) (\int_{c}^{d} h (y) d y)

Justify this claim by showing how to express the double integral from the left side of the equation as an iterated integral and then rearrange it into the product on the right side.

Problem 4

Evaluate

\int_{0}^{3} \int_{0}^{2} \int_{0}^{1} \int_{0}^{z} d w d z d y d x

Give an interpretation of this integral as a “volume” (or, technically, hypervolume) that helps you make sense of the value you calculated.

Follow-Up

I will grade this exercise during an individual meeting with you. That meeting should happen on or before the “Grade By” date above. During the meeting I will look at your solution, ask you any questions I have about it, answer questions you have, etc. Sign up for the meeting via Google calendar. Please have a written solution to the exercise ready to share with me during your meeting, as that will speed the process along.