SUNY Geneseo Department of Mathematics

Divergence

Friday, December 2

Math 223 01
Fall 2022
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Anything You Want to Talk About?

(No.)

Final Exam Time

The current plan is to use our final exam time (Tuesday, December 20, 8:00 - 11:20) for grading meetings.

That time will show as “Busy” on my calendar, but go ahead and ask for appointments during it. As long as the invitations come from someone in this class (and don’t conflict with someone else in the class) I’ll accept them.

Divergence

From “Divergence” in section 5.5 of the textbook.

Key Ideas

The formula for divergence:

Divergence of vector P Q et cetera is derivative of P with respect to X plus derivative of Q with respect to Y et cetera

Divergence has a notation based on the same “nabla” that’s used for gradient. There’s a metaphor (but not exactly a mathematical meaning) in this notation that helps you remember formulas through their similarities to scalar, dot, and (for curl, coming up on Monday) cross products:

Gradient looks like scalar product of vector of differentiations with function, divergence like dot product

Divergence measures flow away from points. 0 means no net flow, positive means flow away from a point, negative means flow towards a point.

Source free fields have divergence 0.

Applications: magnetic fields have divergence 0.

Examples and Applications

Find some divergences. In all cases, this amounts to taking partial derivatives of the components of the vector field and adding them together:

Examples of divergence as sum of derivatives of components with respect to X, Y, Z

My beer-brewing example found that flux across my bag of grains is 0; if divergence measures the tendency of a vector field to flow away from a point, the divergence of the flow field (F(x,y) =⟨ -y, x ⟩) at the center of the bag should also be 0. Is it?

Yes. And we didn’t even need to plug (2,0) into the divergence, because it’s 0 everywhere:

Field with components negative Y and X has divergence 0 plus 0 which equals 0

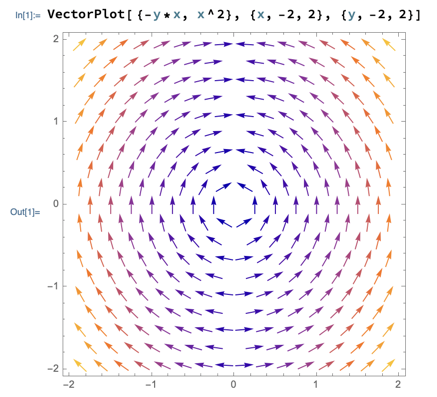
Can the field F(x,y) =⟨ -yx, x2 ⟩ be source free?

No, because it’s divergence isn’t always 0:

Divergence is negative Y minus 0 which is not 0, so field not source free

If field F above represents the flow of water over a surface, which point(s) is water dispersing away from, which is it concentrating towards, and where is it exactly balanced so as to be neither concentrating nor dispersing?

Use the sign of divergence to find that the flow is converging for all points where y > 0, diverging for all points with y < 0, and doing neither along the x axis, where y = 0:

Divergence greater than 0 means flow away, less than 0 means flow towards, equal 0 means no net flow

You can see the flow patterns visually in a plot of the field. The pattern is particularly pronounced along the y axis:

Plot of vectors pulling away from negative Y axis, arcing upward, and converging on positive Y axis

Next

Curl.

Please read “Curl” in section 5.5.

Next Lecture