Some Applications of Multivariable Integrals

Return to Course Outline

Previous Lecture

Anything You Want to Talk About?

(No.)

Some Applications of Multivariable Integration

Based on “Applications of Double Integrals” in section 4.1 of the textbook.

Questions

How do you find bounds for integrals?

Sometimes the problem gives them to you.

Other times you have to work them out from the context of the problem. For example, imagine a temporary garden building that stretches from y = 0 to y = 12, and has an arched cross section whose height (in feet) is given by h = 9 - x²:

If you wanted to find the volume of this building, you could use the given y bounds (0 ≤ y ≤ 12), but you’d have to work out the bounds on x based on the height formula and the understanding that buildings don’t have negative heights. So the x bounds must be x values that make height 0, which works out to ±3 (shown in the drawing, but because we calculated those numbers, not because they were there to begin with).

Key Ideas

Calculate the area of a region by integrating 1 over that region.

The average value of a function over a region is the integral of the function over that region divided by the area of the region.

The volume under a surface f(x,y) is the integral of f over the region of interest.

Examples

Find the volume under one peak of the “egg-carton” z = sin x cos y, 0 ≤ x ≤ π, -π/2 ≤ y ≤ π/2.

Here’s “one peak” plotted by Mathematica, to give you a sense of the volume in question:

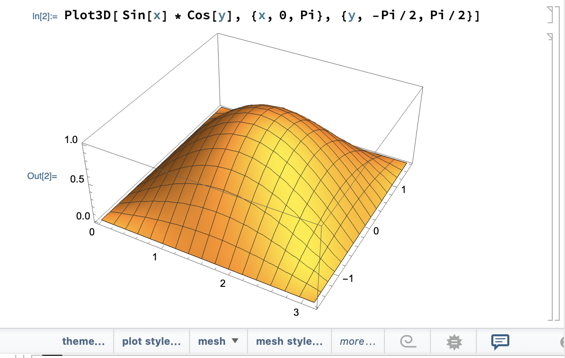
Use the idea that volume is the integral of the function (sin x cos y in this case) over the region of interest (given as 0 ≤ x ≤ π, -π/2 ≤ y ≤ π/2):

What’s the average height of that peak?

Use the idea that the average value of a function is the function’s integral (which we just calculated) divided by the area of the region (which is a square π units on a side):

Next

These volumes and average values, let alone areas, aren’t terribly interesting if they can only be calculated over rectangular regions. So let’s see if there’s a way to evaluate integrals over more general shapes.

Please read “General Regions of Integration,” “Double Integrals over Non-Rectangular Regions,” and “Changing the Order of Integration” in section 4.2 of the textbook.

Next Lecture