Local Extreme Values

Return to Course Outline

Previous Lecture

Anything You Want to Talk About?

(No.)

Field Trip

…to look at partial derivatives, directional derivatives, gradients, etc.

In particular, when you’re standing on the side of a hill…

• Partial derivatives tell you how fast your elevation would change if you were to walk in the x or y directions
• Directional derivatives tell you how fast your elevation would change if you picked some arbitrary direction and walked in it
• Gradients tell you what direction to walk in in order to see the fastest increase in elevation.

Local Extrema

Based on “Critical Points” and “Second Derivative Test” in section 3.7 of the textbook.

Questions

Since critical points can occur at places where derivatives aren’t defined, does that mean they occur at places where the function as a whole is discontinuous? They can, but don’t have to. In particular, a crease or sharp point in the graph of a multivariable function would typically be a place where one or more derivatives don’t exist, but the function is still continuous.

And notice that any interaction between critical points and continuity is separate from the existence of local minimums or maximums: part of the definition of “local minimum” and “local maximum” requires the function to be continuous on a region around the minimum or maximum.

Key Ideas

A critical point is where all derivatives are 0, or one or more derivatives don’t exist.

Extremes can only occur at critical points, although not all critical points have to correspond to extremes.

A second derivative test helps distinguish minima, maxima, and saddle points. It’s more important to know that such a test exists and where to look it and its interpretation up when you need it than to memorize it. But here’s a summary for people who want to look it up here:

A “saddle point” is a point where a surface rises as you approach the point along one dimension, but falls as you approach the point along the perpendicular dimension.

Example

Consider the function f(x,y) = cos x + sin y. It has an interesting shape over the region -π < x,y < π, with, apparently, 1 local maximum and 1 saddle point. Let’s try to figure out where those are.

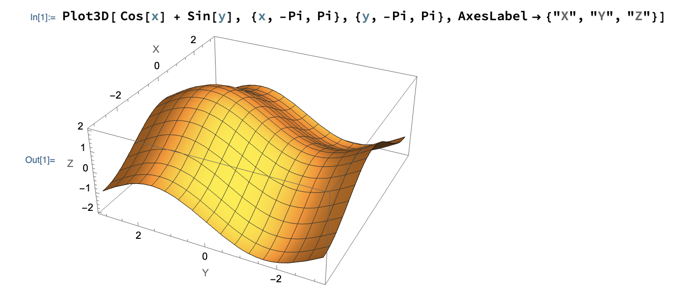
Unlike extreme value problems with 1 variable, this example doesn’t really produce an equation to solve, it produces some x values (actually just one in this case) that make the derivative with respect to x be 0, and some y values that make the derivative with respect to y be 0. So our critical points are all the points you can create by pairing the x value with the y values (Note that this won’t always happen, extreme value problems in multiple variables often lead to equations, or systems of equations, you need to solve.)

Next

See what the second derivative test does with the cos x + sin y function from today.

Absolute minimums and maximums.

Please read “Absolute Maxima and Minima” in section 3.7.

Next Lecture