SUNY Geneseo Department of Mathematics

Limits that Don’t Exist

Wednesday, October 5

Math 223 01
Fall 2022
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Anything You Want to Talk About?

(No.)

Limits that Don’t Exist

From the end of “Limit of a Function of Two Variables” in section 3.2 of the textbook.

Key Ideas

You can show that many limits don’t exist by showing that you get different limits at point P as you approach P along different lines (or curves).

Examples

Show that lim_{(x,y)→(0,0)} x/y doesn’t exist.

One way to show that single-variable limits don’t exist is to show that the limits from the left and right differ. We’re extending that idea to limits that differ as you approach a point on the xy-plane from any of the infinitely many possible directions:

Approaching a limit from left and right with 1 variable versus approaching from any direction with 2 variables

In the case of this particular function, consider x and y approaching the origin along the lines x = y and x = y/2:

As X and Y both approach 0, limit of X over Y is 1 along the X equals Y line but 1 half along X equals Y over 2

Since the limits along these two lines differ, the overall limit doesn’t exist.

To see what such a situation looks like, we plotted z = x/y near the origin in Mathematica. The resulting surface has tears and holes corresponding to places where the function and its limit are undefined. (The gray areas in the plot are places where the surface rises or falls rapidly towards positive or negative infinity, and so Mathematica has clipped it away to be able to plot it.):

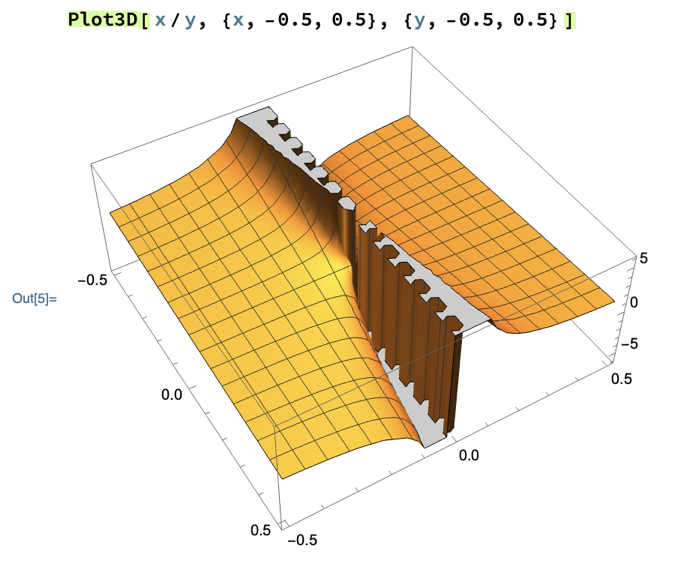
Mathematica plot of X over Y showing tears and holes in surface near origin

You can download the notebook in which we did this if you want to explore it for yourself.

Does lim_{(x,y)→(1,-1)} (x + y) / (2x - 2) exist?

This time it’s a little harder to think of lines to approach along, but a really good guideline is to ask yourself what relationships between x and y, or sometimes what values of either variable, would simplify the function or otherwise make it easy to work with near (1,-1). As you do this, just be careful that you really are describing lines or curves that pass through (1,-1).

We considered three different ways of approaching (1,-1), each one leading to a different value for the limit:

3 different limits of X plus Y all over 2 X minus 2 depending on how X and Y approach point 1 comma negative 1

Now that we know how to work with limits of multivariable functions, we can define and talk about their derivatives.

Please read “Derivatives of a Function of Two Variables” and “Functions of More than Two Variables” in section 3.3 of the textbook.

Next Lecture