SUNY Geneseo Department of Mathematics

3 Dimensional Geometry

Thursday, August 30

Math 223 01
Fall 2018
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

Any prospective math major in their first semester at Geneseo might consider taking Math 101, “Welcome Math Majors.” A 1-credit course that orients you to the math department and its programs. Still time to add it to your schedule during drop-adds.

Questions?

Distances

Basic Idea

What is the distance between points (1,2,1) and (-1,1,3)?

Just plug the coordinates of these points into the distance formula....

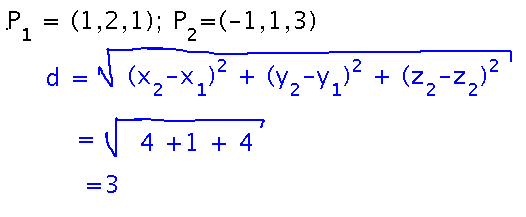
Distance is square root of sum of squares of differences in coordinates, or 3

Applying It

Consider the triangle defined by points (0,0,0), (1,1,0), and (0,0,3). What is the shortest side, and how long is it?

Use the distance formula on every possible pair of points to find the lengths of the sides, then find the shortest.

Use the distance formula on edges (0,0,0) to (0,0,3), (0,0,3) to (1,1,0), and (1,1,0) to (0,0,0) to get lengths 3, sqrt(11), and sqrt(2)

Proof

Paraphrase a proof that the distance from (x1,y1,z1) to (x2,y2,z2) is indeed √((x2-x1)2+(y2-y1)2+(z2-z1)2); see Figure 2.28.

The key idea is to use the Pythagoren theorem on 2 triangles: the desired distance from P1 to P2 is the hypotenuse of one, which has legs of length z2 - z1 and d1. But d1 is the length of a second hypotenuse, this time for a triangle with legs of length x2 - x1 and y2 - y1.

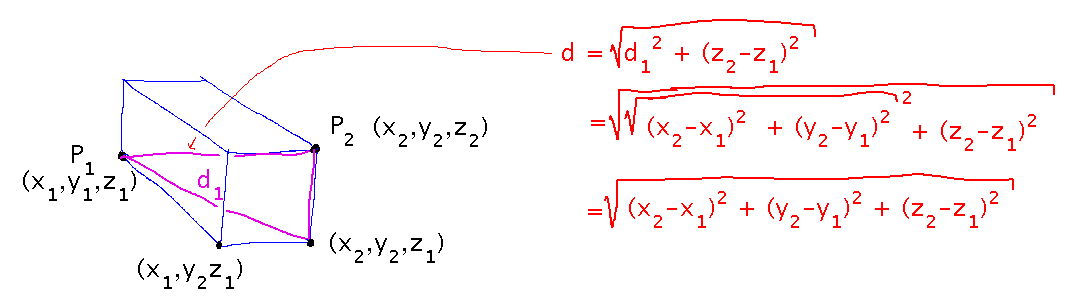
Line from P1 to P2 is the hypotenuse of a triangle whose leg is the hypotenuse of a triangle in the xy plane; use the Pythagorean theorem on each hypotenuse to derive distance formula

4 Dimensions

How far is point (2,4,-1,3) from the origin?

The distance formula extends to any number of dimensions, since the multiple-hypotenuses logic of the proof can be extended to any number of hypotenuses.

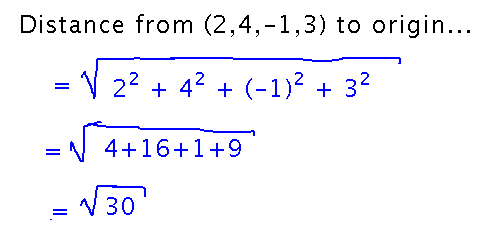
Distance formula with 4 terms: sqrt(2^2+4^2+(-1)^2+3^2) = sqrt(30)

Take-Aways

What the distance formula is and how you apply it.

It does have a reason/proof.

It generalizes to any number of dimensions

Some Simple Surfaces

Planes

Describe the surface defined by z - 3 = 0. A plane parallel to the xy plane, at z = 3

Imagine a 4 dimensional coordinate system with x, y, z, and w coordinates. What sort of region does the equation w = 4 define? A 3D space of infinite extent

Spheres

Do the spheres (x-1)2 + (y+1)2 + z2 = 9 and x2 + (y-1)2 + (z-1)2 = 16 overlap?

Think about this between now and tomorrow and we’ll do it first thing in class.

Take-Aways

What the equations for simple planes look like.

Next

Finish the sphere example, then...

Introduction to Mathematica, especially for plotting in 3 dimensions.

No reading, but...