- Problem set problem 1?
- Theorem 4: if f(n) converges to finite L as n approaches infinity, and an = f(n), then an converges to L
- Application: an = 1/n converges to 0, per theorem
- But not an = n2, although the theorem doesn’t say anything about this case
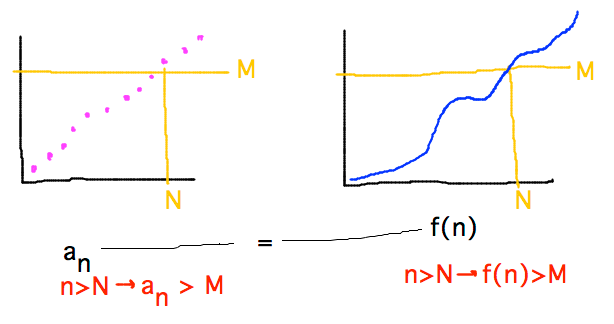
- Does similar thing hold if f(n) approaches ±∞?
- Yes, based on definitions of limits approaching ∞
- Section 10.3
- Completely confusing, epecially proofs
- Reading proofs
- Proofs are central to mathematics, so everyone who studies math needs to see them, and you need to start understanding how they work if you’re going to go much further in math
- But if you’re using mathematical results, the proofs aren’t the first thing you need to understand
- Some people read math twice, skipping proofs and concentrating on identifying key ideas the first time, and reading proofs, examples, etc. the second
- Start by figuring out basic meaning of theorem and how it might be used
- Read proof carefully, paying attention to diagrams, etc.
- Be prepared to fill in skipped steps, explain to yourself how what you’re reading works
- Reading this way isn’t fast!
- Reading proofs
- Completely confusing, epecially proofs
- Examples
- Sum of 1/n3

- Sum of 1/n3
- Convergence tests that compare series
- Read section 10.4 (“Comparison Tests”)