- Exam 1
- Next Tuesday (March 3)
- Material since start of semester (e.g., ln and ex, L’Hôpital’s Rule, inverse trig functions, hyperbolic functions, integration by parts, integration via trig substitution, partial fractions, etc.)
- 4 - 6 short-answer questions, similar to problem set questions
- Whole class period
- Open book, notes, computer for reference; closed person, no CASes
- Colloquium
- “An Elementary Construction of Tessellated Surfaces”
- Jonathan Pakianathan
- University of Rochester
- Monday, March 2, 4:00 - 5:00, Newton 201
- Extra credit for summaries
- Problem set question 1: show the two functions are equal where both are defined
- Question 2: show antiderivative of h is antiderivative of f(x+k)
- Integrate (x2+x+3) / (x2+4)(x-3)
- Note that the partial fraction for the (x2+4) factor has to have an x term as well as a constant in it
- Find A, B, and C coefficients using evaluation at selected values
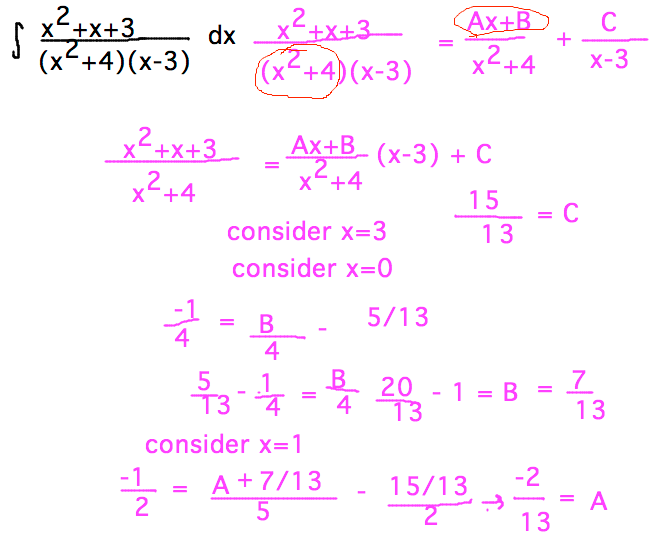
- Plug A, B, and C into partial fraction expansion and integrate
each term

- Integrate x3 / (x2-1)
- This is an improper fraction (numerator is greater than or
equal to denominator), so you have to divide to get a polynomial
quotient and a proper fraction remainder

- Quotient can be integrated via power rule, and remainder via partial fractions
- This is an improper fraction (numerator is greater than or
equal to denominator), so you have to divide to get a polynomial
quotient and a proper fraction remainder
- Numerical integration
- Section 8.7