Problem Set 7 — Applications of Derivatives 1

Purpose

This problem set develops your ability to apply derivatives to solving related rates and extreme value problems. It addresses the following learning outcomes:

• Compute limits and derivatives of algebraic, trigonometric, inverse trigonometric, exponential, logarithmic, and piecewise defined functions (outcome 1)
• Use the derivative of a function to determine the properties of the graph of the function and use the graph of a function to estimate its derivative (outcome 4)
• Solve problems in a range of mathematical applications using the derivative or the integral (outcome 5).

Background

This problem set draws mainly on sections 4.1 (related rates) and 4.3 (extreme values) of our textbook. We discussed related rates in class between October 21 and 23, and extreme values between October 28 and November 2.

Activity

Solve the following problems:

Question 1

(Question 17 from section 4.1 in our textbook.)

The volume of a cube decreases at a rate of 10 cubic meters per second. Find the rate at which the length of the side of the cube changes when the side is 2 meters long.

Question 2

(Inspired by exercises 10 and 11 in section 4.1 of our textbook. The pair is a little unusual as related rates problems, but they are good exercises in calculus- and geometry-based problem-solving.)

A 6-ft tall person walks away from a 10-ft lamppost at a constant rate of 3 ft/sec. See the picture in our textbook for a visual presentation.

Part A

What is the rate at which the tip of the person’s shadow moves away from the person when the person is 10 ft away from the pole?

Part B

What is the rate at which the tip of the person’s shadow moves away from the pole when the person is 10 ft away from the pole?

Question 3

(Exercise 90 in section 4.3 of our textbook.)

Every 2nd degree polynomial, i.e., every function of the form \(y = ax^2 + bx + c\), has exactly one maximum or minimum. You may also have heard that this maximum or minimum occurs at \(x = \frac{-b}{2a}\). Use calculus to derive this result.

Question 4

Here is a graph of some function \(f(x)\). Based on this graph, where in the interval \(-1 < x < 2\) would you estimate that \(f^\prime(x) = 0\)? Where do you think \(f^\prime(x) < 0\)? Where do you think \(f^\prime(x) > 0\)? (Beware that this question asks about \(f^\prime(x)\), not \(f(x)\).)

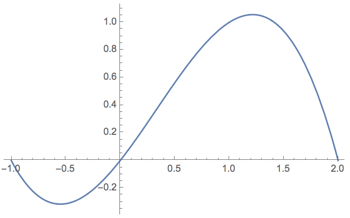
Follow-Up

I will grade this exercise during one of your weekly individual meetings with me. During this meeting I will look at your solution, ask you any questions I have about it, answer questions you have, etc. Sign up for the meeting via Google calendar. Please have a written solution to the exercise ready to share with me during your meeting, as that will speed the process along.