Problem Set 5 — Differentiation Rules

Purpose

This problem set develops your understanding of various differentiation rules, including rules for differentiating trigonometric functions, the chain rule, etc. It addresses the following learning outcomes:

• Compute limits and derivatives of algebraic, trigonometric, inverse trigonometric, exponential, logarithmic, and piecewise defined functions (outcome 1)
• Use the derivative of a function to determine the properties of the graph of the function and use the graph of a function to estimate its derivative (outcome 4)
• Use appropriate modern technology to explore calculus concepts (outcome 7).

Background

This problem set draws mainly on sections 3.5 and 3.6 of our textbook, although parts of it also rely on ideas from earlier sections. We discussed sections 3.5 and 3.6 in classes between October 5 and 9. We talked about taking derivatives in Mathematica in class on September 25.

Activity

Solve the following problems:

Question 1

Find the following derivatives by hand. Notice that some of these are second or higher order derivatives. Then use Mathematica to check your answers.

1. \(\frac{dz}{dx}\) if \(z = 2 \sin\left(x^2\right) - 3 \tan\left(x^3\right)\)
2. \(h^\prime(a)\) and \(h^{\prime\prime}(a)\) if \(h(a) = (a^2+5) \cos a\)
3. \(\frac{dy}{dx}\) if \(y = (6 + \sec (\pi x^2))^2\) (inspired by exercise 236 in section 3.6 of our textbook).

Question 2

(This question goes beyond the expected mastery of limits and derivatives in this course, because it explores a proof of one of the differentiation rules.)

Use the limit definition of the derivative to prove the constant multiple differentiation rule. In other words, show how the equation

can be derived using the limit definition of derivatives.

Question 3

Here is a graph of the equations \(y = \sin x\) and \(y = e^x\) between \(x = -\tfrac{\pi}{2}\) and \(x = \tfrac{\pi}{2}\):

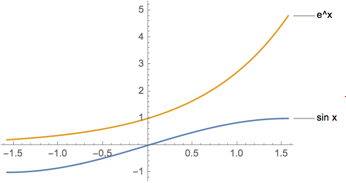
Based on the graph…

1. Where, if anywhere, do you think the derivative of \(\sin x\) is greater than the derivative of \(e^x\)?
2. Where, if anywhere, do you think the derivative of \(\sin x\) is less than the derivative of \(e^x\)?

Note that the questions are asking about the derivatives of the functions in the graph, not the functions themselves. Be sure you can explain why the graph supports your choices.

Finally, check your guesses based on the graphs by comparing the actual derivatives of \(\sin x\) and \(e^x\) at your chosen points. You may use a calculator or similar tool to evaluate the derivatives.

Question 4

(This question goes beyond the expected mastery of the “technology” outcome for this course, because it exposes you to issues that arise in using technology with “real-world” models that are normally beyond the scope of the course.)

In our discussions of the chain rule, we saw the following function for the distance, \(d(t)\), between Earth and Mars over a few days in late March, 2014:

We talked about how the chain rule could be used to find the derivative of this function, but didn't actually do it. This situation is a perfect example of where “real” mathematical modelers would use something like Mathematica to find the derivative. Do so. How can you tell if Mathematica’s result is plausible, i.e., what, if anything, in it reassures you that you typed the right formula into Mathematica and that it was able to find the right derivative? (Hint: consider using the “Simplify” button below Mathematica’s output to put the initial result into a form that’s easier to read.)

Follow-Up

I will grade this exercise during one of your weekly individual meetings with me. During this meeting I will look at your solution, ask you any questions I have about it, answer questions you have, etc. Sign up for the meeting via Google calendar. Please have a written solution to the exercise ready to share with me during your meeting, as that will speed the process along.