Math 221 02 2nd Integration Exercise

Purpose

This problem set develops your understanding of methods and applications of integration. The problem set addresses the following learning outcomes:

Compute definite and indefinite integrals of algebraic, trigonometric, inverse trigonometric, exponential, logarithmic, and piecewise defined functions (outcome 2)
Solve problems in a range of mathematical applications using the derivative or the integral (outcome 5)
Apply the Fundamental Theorem of Calculus (outcome 6)
Use appropriate modern technology to explore calculus concepts (outcome 7).

Background

This problem set is based on sections 5.5, 6.1, and 6.2 of our textbook. We talked about section 5.5 (substitution) in classes and related readings and online discussions between November 23 and December 2. We studied section 6.1 (area between curves) in readings and discussions between December 2 and 7, and will study section 6.2 (volume by slicing) between December 7 and 9.

In addition to the material in the textbook, this problem set also asks you to evaluate integrals with Mathematica. That is covered in the class notes from November 23.

Activity

Solve the following problems:

Question 1

Evaluate each of the following definite or indefinite integrals. After evaluating each by hand, check your answer by evaluating the integral with Mathematica.

Part A

(Exercise 292 in section 5.5 of our textbook.)

\int_{0}^{1} x \sqrt{1 - x^{2}} d x

Part B

(Exercise 296 in section 5.5 of our textbook.)

\int_{0}^{\frac{π}{4}} \sec^{2} Θ \tan Θ d Θ

Question 2

(Based on exercise 3 in section 6.1 of our textbook.)

Use Mathematica to find the area between the curves $y = x^{3}$ and $y = x^{2} + x$ , as shown in the following graph:

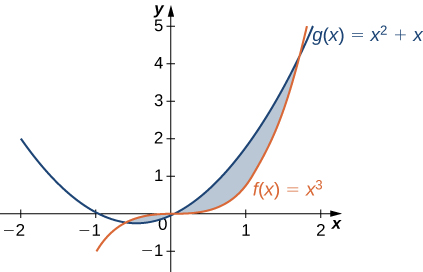
x cubed and x squared plus x cross at 3 points

Question 3

(This question goes beyond the expected mastery of integration (outcome 2) because it asks you to prove an integration rule.)

Suppose that $f (x)$ is an integrable function, and that

\int f (x) d x = F (x) + C

Show that for all constants $a$ ,

\int f (x + a) d x = F (x + a) + C

Question 4

During our Zoom discussion of areas between curves, we briefly talked about volume, and in particular the idea that if you take an arbitrary region of area $A$ and extrude it for distance $h$ perpendicular to itself, the volume of the resulting shape is

V = A h (Equation 1)

This diagram might help illustrate what it means to “extrude” a region in such a manner:

Area A extends for distance h in third dimension

Part A

(This question goes beyond the expected mastery of applications of integrals (outcome 5) by asking you to use integration to derive a general geometric formula.)

Use Section 6.2’s “slicing method” to derive Equation 1.

Part B

From Equation 1, the derivative of an extruded volume with respect to height is its cross-sectional area, i.e.,

\frac{d V}{d h} = A

Show that this is also what part 1 of the Fundamental Theorem of Calculus gives if applied to the volume integral you found in Part A.

Follow-Up

I will grade this exercise during one of your weekly individual meetings with me. During this meeting I will look at your solution, ask you any questions I have about it, answer questions you have, etc. Sign up for the meeting via Google calendar. Please have a written solution to the exercise ready to share with me during your meeting, as that will speed the process along.