SUNY Geneseo Department of Mathematics

Problem Set 10 — Integrals

Math 221 02
Fall 2020
Prof. Doug Baldwin

November 30 - December 4

Purpose

This problem set develops your understanding of integrals broadly, including summations and integrals’ definition as limits of summations, the Fundamental Theorem of calculus, and the resulting relationship between definite integrals and antiderivatives. The problem set addresses the following learning outcomes:

Compute limits and derivatives of algebraic, trigonometric, inverse trigonometric, exponential, logarithmic, and piecewise defined functions (outcome 1)
Compute definite and indefinite integrals of algebraic, trigonometric, inverse trigonometric, exponential, logarithmic, and piecewise defined functions (outcome 2)
Apply the Fundamental Theorem of Calculus (outcome 6).

Background

This problem set is based on sections 5.1 through 5.3 of our textbook. We talked about those sections in classes between November 13 and 20.

Activity

Solve the following problems:

Question 1

(Based on problem 10 in section 5.1 of our textbook.)

Use algebraic rules and closed form formulas for summations to evaluate the sum

\[\sum_{j=11}^{20}(j^2-10j)\]

Also write the sum as an explicit sum of numbers, although you don’t have to evaluate this explicit sum. You may use a calculator for the purely numeric parts of this problem, but not to simplify the sum.

Question 2

Part A

Approximate the definite integral

\[\int_1^2 \frac{1}{2} x\,dx\]

using a Riemann sum with 100 intervals. Use a right-endpoint approximation. (Notice that this integral starts at 1, whereas similar examples in class generally started at 0 — so be sure you understand how Riemann sums take the bounds of integration into account, and, of course, ask if you have any questions. I recommend that you use closed form formulas and algebraic rules for summations to simplify the Riemann sum rather than just trying to evaluate it by brute force, although you can use a calculator for the final numeric calculations.)

Part B

Find the exact value of the definite integral in Part A by taking the limit of the Riemann sum from that part.

Question 3

(Exercise 160, parts a and b, in section 5.3 of our textbook.)

Given a graph of \(y = \int_0^x f(t)\,dt\) for some piecewise constant function \(f\), find the intervals over which \(f\) is positive, negative, and zero; also find the minimum and maximum values of \(f\). The graph from the textbook is as follows (beware that this graph shows \(y\) but the question asks about \(f\)).

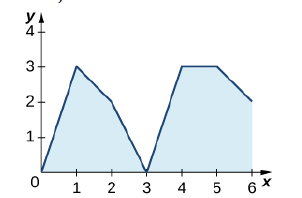
Graph rising linearly from 0 0 to 1 3 then down to 2 2 and 3 0, up to 4 3, flat to 5 3, down to 6 2

Question 4

(Exercise 180 in section 5.3 of our textbook.)

Evaluate

\[\int_1^4 \frac{2-\sqrt{t}}{t^2}\,dt\]

Follow-Up

I will grade this exercise during one of your weekly individual meetings with me. During this meeting I will look at your solution, ask you any questions I have about it, answer questions you have, etc. Sign up for the meeting via Google calendar. Please have a written solution to the exercise ready to share with me during your meeting, as that will speed the process along.