Problem Set 1 — Limits

Purpose

This problem set familiarizes you with the concept of a limit, and with some ways of using technology related to limits.

This problem set addresses the following learning outcomes:

• “Limits and Derivatives,” outcome number 1
• “Technology,” outcome number 7.

Background

This problem set draws on the “Intuitive Definition of a Limit” subsection of section 2.2 in our textbook. It also requires you to use Mathematica to plot graphs, and Mathematica or other technology to evaluate functions. All of this material was covered in class on September 3 and 4.

Activity

Solve the following problems:

Question 1

(Expanding on Exercises 32 through 34 in section 2.2 of Calculus Volume 1 for SUNY Geneseo)

Part A

Generate a table of values of the function \(f(x) = (x+1)^{\tfrac{1}{x}}\) for \(x = -0.01\), \(-0.001\), \(-0.0001\), \(-0.00001\), \(0.00001\), \(0.0001\), \(0.001\), and \(0.01\). Use Mathematica or other technology in answering this question (I’d recommend a spreadsheet as the ideal technological tool here, but you can use something else if you prefer).

Part B

Based on this table, estimate the value of \(\lim_{x \to 0}(x+1)^{\tfrac{1}{x}}\).

Part C

Use Mathematica to plot \((x+1)^{\tfrac{1}{x}}\) for \(x\) ranging from \(-0.1\) to \(0.1\); explain why this graph is or is not consistent with the limit you estimated from the table.

Part D

(This part exceeds what you need in order to meet the learning outcomes for this question, because it asks you to connect a limit to other areas of math.) What often-used mathematical constant does \(\lim_{x \to 0}(x+1)^{\tfrac{1}{x}}\) equal? Give the name of the constant.

Question 2

Consider the function

Part A

Using Mathematica or other technology, calculate enough values of \(g(t)\) near \(t=2\) to estimate what \(\lim_{t \to 2} g(t)\) is.

Part B

Use Mathematica to plot \(g(t)\) over a small range of values covering \(t=2\) (I used the interval \([1.5,2.5]\)) and estimate the limit from your plot.

Question 3

Here is a graph of a function \(f(x)\):

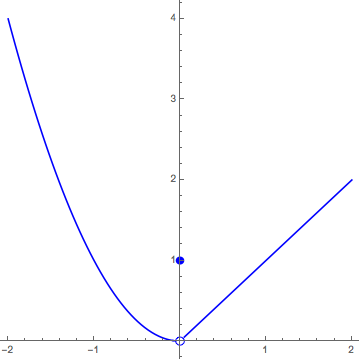
Part A

Based on this graph, what do you estimate \(\lim_{x \to -1}f(x)\) to be?

Part B

Based on this graph, what do you estimate \(\lim_{x \to 0}f(x)\) to be?

Part C

Based on this graph, what are \(f(-1)\) and \(f(0)\)?

Question 4

Sketch a graph over the interval \([0,4]\) of a function \(f(x)\) that has the following features:

1. \(f(0) = f(4) = 0\).
2. \(f(1)\) is defined and equals \(\lim_{x \to 1}f(x)\).
3. \(f(2)\) is undefined, but \(\lim_{x \to 2}f(x)\) is defined.
4. \(f(3)\) is defined, and \(\lim_{x \to 3}f(x)\) is also defined, but \(f(3) \ne \lim_{x \to 3}f(x)\).

Note that I’m only asking you to sketch a graph of such a function, not find an equation that defines it.

Follow-Up

I will grade this exercise during one of your weekly individual meetings with me. During this meeting I will look at your solution, ask you any questions I have about it, answer questions you have, etc. Sign up for the meeting via Google calendar. Please have a written solution to the exercise ready to share with me during your meeting, as that will speed the process along.