SUNY Geneseo Department of Mathematics
Math 221 02
Fall 2020
Prof. Doug Baldwin
This discussion reinforces some of the intuition behind limits that section 2.2 of the textbook presents. In particular, see the “Intuitive Definition of Limit” and “The Existence of a Limit” subsections for background on this discussion.
As usual, post responses to one or more of the following prompts. You may also respond to other people’s responses, of course. Make your posts before class time on Friday, September 4.
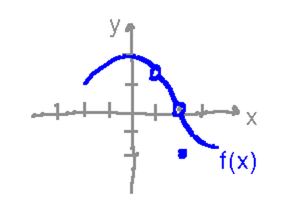
Particularly when discussing limits, the textbook uses some conventions about graphs of functions that it doesn’t define (at least not in chapter 2), but that hopefully make sense. To make sure they make sense, here is a roughly sketched graph of a function that uses the same conventions:
What, if anything, can you say about the value of f(0)? How do you know?
What, if anything, can you say about the value of f(1)? How do you know?
What, if anything, can you say about the value of f(2)? How do you know?
Consider the function
\[f(x) = \frac{x^3-3x^2+3x-1}{x-1}\]Notice that you cannot calculate \(f(1)\) from this equation, because doing so would involve dividing by 0. But you can find the limit as x approaches 1. This Google spreadsheet will help you do so. You should all be able to add things to the spreadsheet. It’s set up as a column of \(x\) values, a column of corresponding \(f(x)\) values, and a plot of the \((x, f(x))\) curve defined by those two columns. As an example, I’ve entered one \(x\) value into the “x” column so you can see the corresponding \(f(x)\) value, and all of 1 point in the plot. You can now extend this by adding other values to the shaded pink area in the “x” column; the “f(x)” column and plot should update automatically. But note that in order for the plot to make sense, values in the “x” column need to be in increasing order.
Ideally you will use the spreadsheet to collaboratively explore the function and speculate about its limit, i.e., each person will add a few numbers to the spreadsheet, post here about what they see and what it means for the limit, the next person will put some more numbers into the spreadsheet and post new observations, etc. But even if things don’t happen quite that way, please do comment on each other’s ideas about the limit, ask questions about them, suggest extensions or variations, etc.
Consider the function
\[g(t) = \frac{t^2 - 4}{t+2}\]Similar to Part 2, you can’t evaluate this function directly at \(t = -2\) because of division by 0. Also similar to Part 2, but without a spreadsheet set up to help, see if you can estimate the limit of \(g(t)\) as \(t\) approaches \(-2\). Once again, I hope this can be a collaborative effort, for example that each of several people can work out and post a few values apiece of \(g(t)\), from which others can estimate a limit, yet others can ask questions or suggest further things that would be helpful to do, etc.
Use a table of values and/or a graph to determine whether
\[\lim_{y \to 0} \frac{|y|}{y}\](i.e., the limit as \(y\) approaches 0 of the absolute value of \(y\) divided by \(y\)) exists, and if so, what it is.