Differentiation Miscellany Discussion

This discussion helps you understand a collection of topics related to derivatives that we can talk about now that we know some differentiation rules. These topics include higher-order derivatives, antiderivatives, and visual relationships between functions and their derivatives. Some of this is discussed in “Graphing a Derivative” and “Higher-Order Derivatives” in section 3.2 of our textbook. All of it (plus derivatives in Mathematica) will be topics we talk about in class on Friday (September 25).

Post at least one response to at least one of the following by class time on Friday:

Higher-Order Derivatives

What is the second derivative of f(x) = x² - 6x + 2? How about the third derivative? The fourth?

How many derivatives (i.e., first derivative, second derivative, third derivative, etc.) can you take of x⁴ - 2x² + 7 before the result stops changing, i.e., before taking more derivatives just gives you the result you already have?

In general, how many derivatives can you take of a degree-n polynomial (i.e., a function of the form f(x) = a_nxⁿ + a_n-1x^n-1 + … + a₁x + a₀ before the derivatives stop changing? What value does the derivative have when it stops changing?

Antiderivatives

Find a function whose derivative is 2x + 1. How about a function whose derivative is 6x² + 4x + 2?

Can you find more than one function to answer each part of the above question? If so, give some examples. Can you put into words some general pattern or rule that explains either why there are multiple answers to the questions, or why there cannot be, depending on which you think is the case?

Graphs and Derivatives

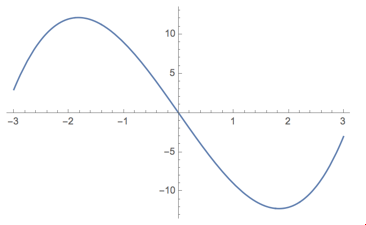
Here is a graph of a certain function:

Based on this graph, where would you say the derivative is positive? Where is it negative? Zero?

Where do you think the derivative has its most positive value? What about its most negative value?