Area between Curves Discussion

(The following is/are the initial prompt(s) for an online discussion; students may have posted responses, and prompts for further discussion may have been added, but these things are not shown.)

Finding the area between 2 curves is one of the first extensions of definite integrals beyond finding the area under a single curve. Section 6.1 of our textbook talks about this application; the following examples give you a chance to try the ideas and share your results or thoughts.

Simple Forms of the Problem

To get taste of the basic idea, see if you can find the area between the curves y = x³ and y = x² over the interval 1 ≤ x ≤ 2. How would you do this, and what result do you get?

Area-between-curves problems get a little more interesting when the region is defined by where the curves intersect. Such problems are often described simply as “the area between f(x) and g(x)” for given functions f(x) and g(x); the implication is that the desired area is bounded on the left and right between points where f(x) = g(x). For example, how would you find the area between the curves y = x² and y = 1 - x²?

More Complicated Forms

Taking the ideas a little beyond what’s in most textbooks, what if one or both functions are defined piecewise or have a finite number of discontinuities? For example, suppose f(x) = x² - 1 and g(x) is defined by

How would you find the area between the graphs of f(x) and g(x) over the interval -2 ≤ x ≤ 1? What, if anything, does your answer suggest about integrating discontinuous functions generally?

A common variation (which does appear in most textbooks) is to have curves that cross one or more times in the interval of interest. For example, can you find the area between the curves y = x³ and y = x² over the interval 0 ≤ x ≤ 2?

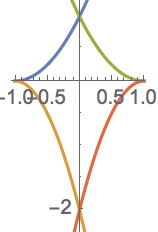
You can also apply ideas of areas between curves to areas that are bounded by multiple curves. For example, the enclosed area below that looks vaguely like a kite with curved edges or a cross-section of a spinning top is the area bounded by the curves y = (x+1)², y = -2(x+1)², y = (x-1)², and y = -2(x-1)²:

What is its area?