SUNY Geneseo Department of Mathematics
Monday, September 14
Math 221 02
Fall 2020
Prof. Doug Baldwin
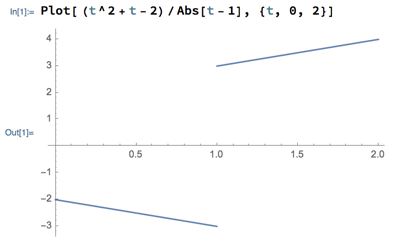
Can Mathematica calculate absolute values, for example if one wanted to plot the functions involving absolute value from the one-sided limits discussion?
Yes indeed. Mathematica has a built-in Abs function that takes absolute values. So here is how you could use it to plot the function from the discussion:
Don’t forget to set up weekly meetings with me. Make appointments a few days in advance to be sure times are available.
Also, to the extent you can, try not to leave gaps too small for someone else to use between appointments. For example, if there’s an appointment that ends at 9:20 and you can see me then, don’t make yours for 9:30.
The next session is tomorrow (Tuesday), 4:00 - 5:30
Recordings of SI sessions are now on Google drive. Check Emiliana’s announcements for where.
Key idea: Mathematica has a Limit function that finds limits.
This function has two arguments, the expression whose limit you want to find, and a description of where to find that limit, of the form var -> value, where var is the variable in the expression and value is the value that variable is approaching for the limit.
For example...
(This notebook contains both the absolute value example and the limit example, if you want to try them for yourself.)
From the “One-Sided Limits” subsection of section 2.2 in the textbook, and the one-sided limits discussion in Canvas.
1-sided limits can help tell if 2-sided limits do not exist (if the 1-sided limits differ).
1-sided limits can also help find 2-sided limits (if the 1-sided limits are equal).
Algebra and limit laws apply to finding 1-sided limits.
Consider the function defined by
To use definitions like this one, start by figuring out which of the conditions on the right holds for your value of x. Only one should hold. Then plug that x into the corresponding expression. So, for example...
f(0) = 0, because 0 < 1 so the first line of the definition applies and says that f(0) = 0.
f(1.5) = 2.25, because 1.5 is between 1 and 2, so the second line applies and says that f(1.5) = 1.52.
f(2) = 0 because 2 ≥ 2, so the third line applies and says that f(2) = 2 - 2.
f(3) = 1 because the third line applies again, so f(3) = 3 - 2.
f(1) does not exist, because no line applies when x = 1.
Is limx → 1 f(x) defined? If so, what is it? How about the 1-sided limits as x approaches 1 from the left or from the right?
We can’t evaluate the ordinary (2-sided) limit directly, because 2 different parts of the definition would apply, depending on whether we approached 1 from above or below. So we have to evaluate the 1-sided limits. If they are equal, then their common value is also the value of the 2-sided limit. The general strategy for using 1-sided limits to either find a 2-sided limit or show that it doesn’t exist is...
Using this strategy to find limx → 1 f(x) goes as follows:
The limit from the left involves x approaching 1 from below, i.e., x is always less than 1. So that means we can use the first line of the function’s definition along with any necessary algebra or limit laws to find the limit:
In the limit from above, x is always greater than 1, so use the second line of the definition:
Since these two 1-sided limits are equal, together they imply that the 2-sided limit is also equal to 1:
Is limx → 2 f(x) defined? If so, what is it? How about the 1-sided limits as x approaches 2 from the left or from the right?
This proceeds very much like the limits as x approaches 1, except that we use lines 2 and 3 of the definition, and the 1-sided limits differ, so the conclusion is that the 2-sided limit does not exist:
What are
and
To find these limits, notice that absolute value can be defined piecewise. Then limits involving it fit into the above scheme of deciding which piece applies as the variable approaches the given value from the left and/or right.
Now to find the limit from the left, notice that approaching 1 from the left means that x is always less than 1, so x-1 is always negative. Thus, the first line of the piecewise definition of absolute value applies. After using it, we’re taking the limit of a function that will behave the same way from left and right, and we can use the usual algebraic methods and limit laws:
To find the limit from the right, x will be greater than 1, so x-1 is greater than 0 and the third line of the piecewise definition of absolute value holds:
Some of you have probably seen “vertical asymptotes,” i.e., places where a function’s value rises to infinity (or falls to negative infinity), like these:
There would seem to be useful ways to talk about such asymptotes as limits, but we haven’t really seen that, or looked at limit laws that would let us do it. So let’s fix that.
Please read “Infinite Limits” in section 2.2 of the book.
Please also follow and contribute to this discussion.