Integration by Substitution

Return to Course Outline

Previous Lecture

Misc

Colloquium

Jamie Juul, Amherst College (faculty candidate).

Monday, November 20, 4:00 PM, Newton 201.

I don’t know the topic yet.

Extra credit for writing a paragraph about connections you make to it, as usual.

Questions?

Problem 4, Problem set 9

How to start on “limit of Riemann sum”?

Start by identifying what function you’re using, what x values appear in the sum, and what the change in x over each sub-interval is. Keep in mind that the sum corresponds to an integral of f(x) over the interval [a,b].

To find the x’s for a uniform sub-interval of width Δx, use the right endpoints and note that the right endpoint of interval i is a + i Δx.

Integration by Substitution

Section 5.5

Problem set.

Antiderivatives

Find the antiderivatives of 2x / √(x² - 3).

The main helpful idea from the reading is the strategy for integration by substitution:

1. Find g(x) in the integrand such that g′(x) is also in the integrand; let u = g(x).
2. Substitute u for g(x) and du for g′(x) in the integrand.
3. Integrate with respect to u.
4. Substitute the definition of g back into the integral you got.

Start by identifying a promising-looking u and du:

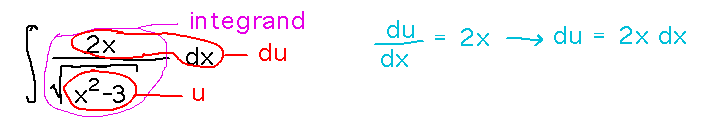
Then express the integral in terms of u and du:

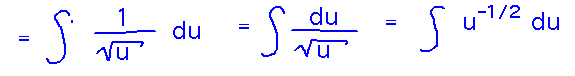
Finally integrate with respect to u, and replace u with x² - 3 in the result:

Find the antiderivatives of sinx cosx.

Find a promising u and du:

Express the integral in terms of u and integrate:

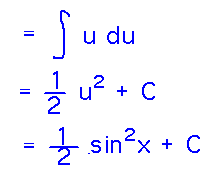
Notice that this is only the most natural of several substitutions that could all be used to evaluate this antiderivative:

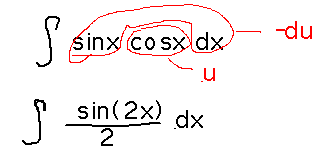
Try integrating sinx cosx by using u = cosx.

Notice that du involves a negative that’s not present in the original integrand. But we can still integrate with respect to u, and compensate for the negative by negating the result:

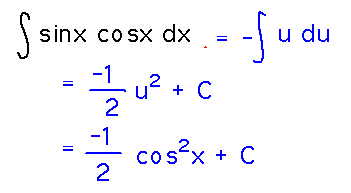
Are that result and yesterday’s sin²x / 2 really both antiderivatives of sinx cosx? Check by differentiating both:

Notice that the key to finding both derivatives was the chain rule. That’s not an accident, integration by substitution is basically the integration rule that inverts the chain rule.

How is it possible that two different functions are both “the” antiderivative of sinx cosx?

Maybe it has to do with sinx and cosx both having similar graphs? But the graphs are displaced relative to each other, cosine isn’t just a scaled sine or such:

But of course we aren’t dealing with sinx and cosx, we’re dealing with their squares. Maybe that helps?

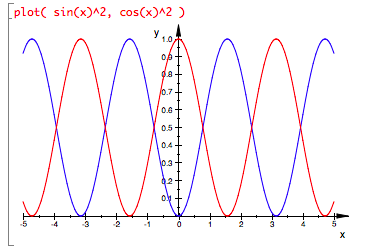
The two curves still aren’t the same function, they’re mirror images of each other. But they still aren’t the antiderivatives we got, either. We need to negate the cosine curve (and scale both by 1/2):

Now they are just vertically shifted copies of each other.

That’s the “+ C” in antiderivatives in action: sometimes it allows two superficially very different functions to both be antiderivatives of the same thing. And in fact, we can work out what C makes one of the functions equal the other in this case:

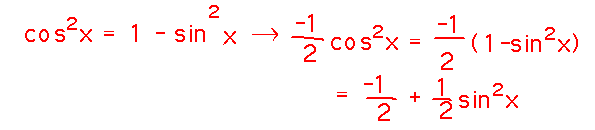
Find the antiderivatives of √(2x+1).

Start by identifying u and du. The only real choice is u = 2x+1 and du = 2dx:

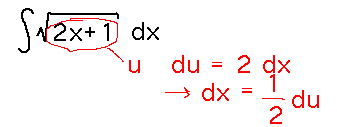
But there’s no 2 in the integrand to match the “2dx.” One way to deal with this would be to realize that du = 2dx implies that dx = du/2, and so substitute 1/2 du for dx:

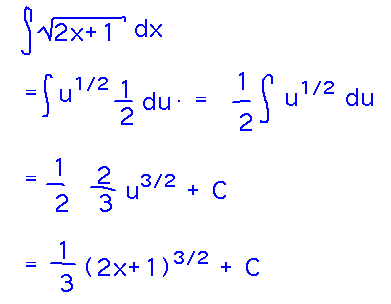
Another way to match du to a 2dx and explain multiplying by 1/2 at the end is to multiply the integrand by 2/2 and then factor out the denominator:

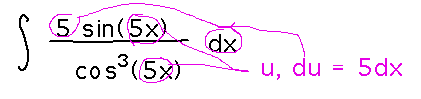
Find the antiderivatives of 5 sin(5x) / cos³(5x). As usual, start by finding a promising u. In this case, u = 5x and thus du = 5 dx looks like a good choice:

The integrand is simpler now, but it’s still not obvious how to integrate it. But factoring it into 2 recognizable trigonometric functions helps (in general, rewriting an integrand into a new form often helps you evaluate integrals):

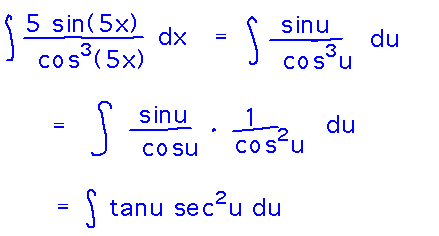
In this form, another substitution stands out. There’s nothing wrong with using multiple substitutions to evaluate an integral.

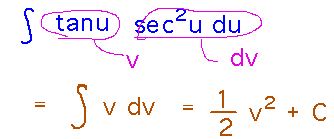
Finally, undo the substitutions to get the antiderivative in terms of the original variable x:

Another substitution that could start this problem would be u = cos(5x). This requires using the chain rule to find du, but lets you evaluate the integral with only one substitution.

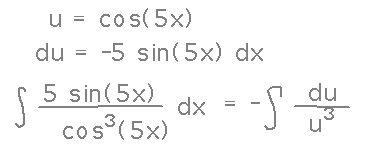
Definite Integrals

Integrate √(x⁴-x²) from 1 to 3. A good way to start is to rewrite the integrand in order to make a useful substitution evident:

Now carry out the substitution, but also apply it to the bounds. For instance, when x = 1, u is x²-1 = 1²-1 = 0; when x = 3, u = 3²-1 = 8.

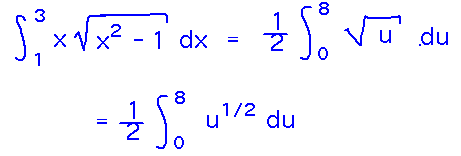
Now you can find the antiderivative and evaluate between the u bounds, without having to reverse the substitution and express the result in terms of x. This is a nice payoff from putting the bounds in terms of u when you did the substitution.

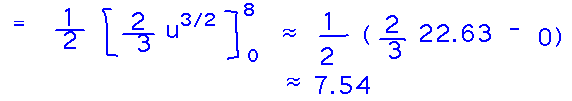
Take-Aways

Substitution can be a good way to evaluate an integral when the integrand is a product of a function and its derivative.

The integrand doesn’t even have to be an exact product, just close enough that multiplying by a constant makes it exact.

It can be helpful to make multiple substitutions sometimes.

When using substitution to evaluate a definite integral, apply the substitution to the bounds too.

Next

Applications of integration: area between curves.

Read section 6.1.

Next Lecture