Geneseo Math 221 05 Optimization

Misc

Colloquium

“Introduction to Catastrophe Modeling”

Raymond Cook, AIR Worldwide

Thursday, November 2, 4:00 pm

Newton 203

Extra credit for writing a paragraph on connections you make to the talk.

Grading Appointments

It’s the time of the semester when they become a scarce resource, so...

If you have one but can’t make it, please delete it as early as possible through Google calendar so other students can have the time.
But don’t make and then cancel an appointment in the first place if at all possible.
And remember to sign up early for appointments so you don’t get closed out.

Exam 2

Thursday, November 2

It will cover material not tested on the first exam, for example the chain rule, implicit differentiation, related rates, linear approximations, extrema, shapes of curves, limits at infinity and asymptotes, etc.

The rules and format will otherwise be similar to the first exam, especially “open-references, closed-person.”

Questions?

Optimization

Section 4.7

Warm-Up

Take (or at least imagine taking) a sheet of paper, 8.5 by 11 inches. If you can cut it up and tape the pieces back together any way you like, what’s the largest volume tube you can make?

Volume is dominated by radius squared, so giving up height for radius until you get an infinitely short tube of infinite radius maximizes volume

Examples

Eco preserve. Ecological preserves should have a minimal perimeter, because that perimeter is what “foreign” species enter across. If you’re designing a rectangular preserve with area 10 square miles, how long should the sides be to minimize perimeter?

Reading ideas re process for solving optimization problems:

Define variables that represent the quantities in the problem, set up a formula that gives the value to optimize in terms of the other variables. In this problem, for example, quantities are the lengths of the sides, the area, the perimeter; you want to minimize perimeter.
Differentiate the expression for the value to optimize (perimeter in this case).
Set that derivative equal to 0 and solve for the other variable(s).
Use the solution from step 3 to find values for the optimized variable and any others that didn’t appear in the derivative but that are expressed in terms of the one(s) that did.
Check the endpoints of the independent variable(s) domain to be sure the optimum doesn’t appear at them (as, for instance, it did in the tube example at the beginning of class).

With sides y and x = 10/y, dP/dy = 2 - 20/y^2 = 0 at y = sqrt(10)

Lawn mower. I somehow manage to finish mowing my lawn in the corner furthest from the shed the lawn mower lives in. If the lawn is a 50 foot by 100 foot rectangle with a driveway along one side, and I can push the mower at a speed of 1 ft/sec on the lawn and 3 ft/sec on the driveway, where should I aim in order to put the lawn mower away quickest?

Pushing at 1 ft/sec on grass vs 3 ft/sec on driveway yields optimal route about 83% on driveway.

Buckets. Do bucket manufacturers (or at least the manufacturer of one particular bucket) minimize the amount of plastic they use to make their buckets?

Treat the bucket as a cylinder, and minimize its surface area given a fixed volume. Note that the key difference mathematically between this and the tubes from last time is that surface area now has an r² term.

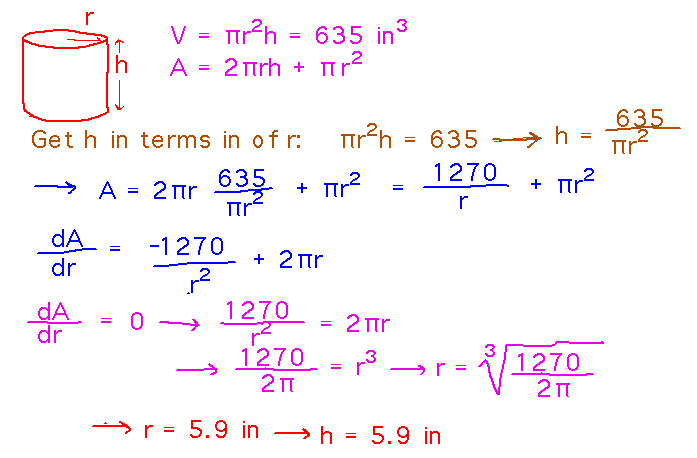
Optimal radius and height for a 635 cu in bucket are r = h = 5.9

Eco preserve revisted. Suppose the preserve has a river along one side, which is impassable to invasive species and so needn’t be counted in the perimeter. What then are the height and width that minimize perimeter?
Minimizing 2a + b subject to ab = 10 yields a = sqrt(5), b = 2 sqrt(5)

Take-Aways

Optimization is finding extreme values, but with constraints that relate the variables involved and/or restrict the domain.

The process for finding optimum values (see above).

Problem Set

See handout

Calculating area under a curve — integration.

Read section 5.1 for Wednesday, November 1.