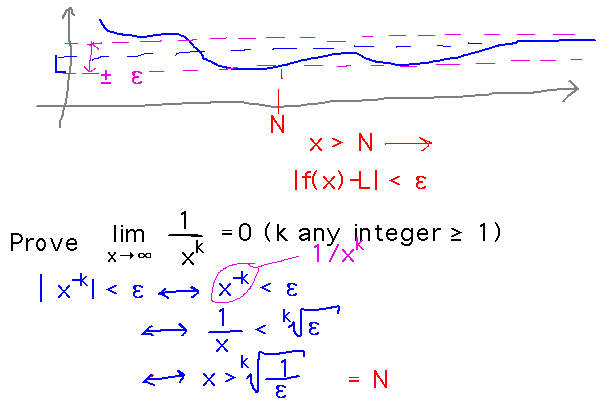
SUNY Geneseo Department of Mathematics
Monday, October 23 - Wednesday, October 25
Math 221 05
Fall 2017
Prof. Doug Baldwin
Please return questionnaires by Friday (Oct. 27), if you want to return them.
Mostly covers extreme values, shapes of graphs, etc.
See handout for details.
Section 4.6
Examples. Find limx→∞ (2x2 - 3x)/(x2+1)
Describe the end behavior of f(x) = x sinx
Does y = (3x + 2)/5x have any horizontal asymptotes? If so, where? What about oblique asymptotes?
Commonalities. What common idea from the reading underlies solving all of these problems (and similar ones)?
Like many other kinds of limits, working with limits as x approaches ∞ is best done by identifying a few relevant laws and then trying to use algebra or other laws to rewrite specific limit problems into forms to which those laws apply.
One major law is that limx→∞ (1/xk) = 0. Prove it.
Reading idea: limx→∞ (f(x)) = L if for all ε, there exists an N such that if x > N, then |f(x)-L| < ε
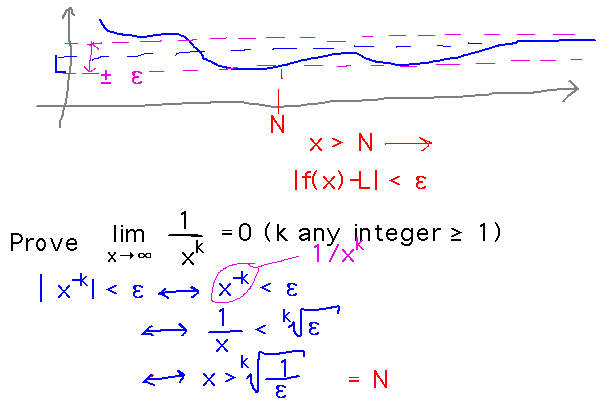
Finding limits. Find limx→∞ (2x2 - 3x) / (x2 + 1)
Reading idea: When the numerator and denominator of a ratio of polynomials have the same degree, the limit is just the ratio of the coefficients of the highest-degree term. So in this case the limit should be 2.
Verify this by rewriting the limit and using limit laws.
Take-Aways
Two important laws regarding limits as x approaches ∞
Dividing by the highest power in the denominator is generally a good trick for finding limits of rational functions (ratios of polynomials).
Asymptotes.
Finish reading or review section 4.6.