- Hour exam 2
- Tuesday (Nov. 18)
- Covers material from 1st exam through optimization (e.g., chain rule, implicit differentiation, related rates, Mean Value Theorem, curve sketching, extrema and optimization, etc.)
- 6 - 9 short answer questions, including word problems
- Rules and format otherwise similar to 1st exam, especially open references rule
- Review at end of class today
- Related rates example
- Spy raising camera over wall
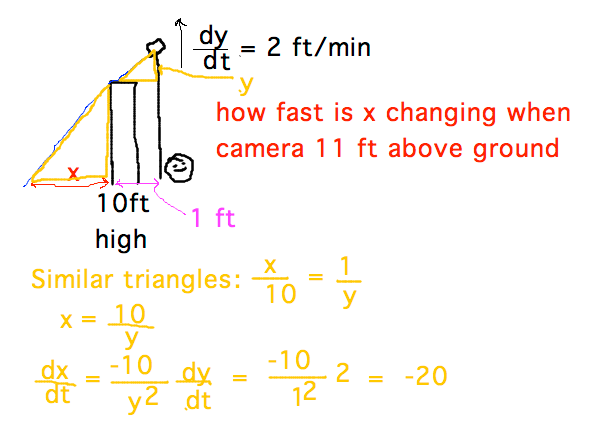
- Spy raising camera over wall
- Optimization example
- Explorer at base of peninsula wants shortest route to shore
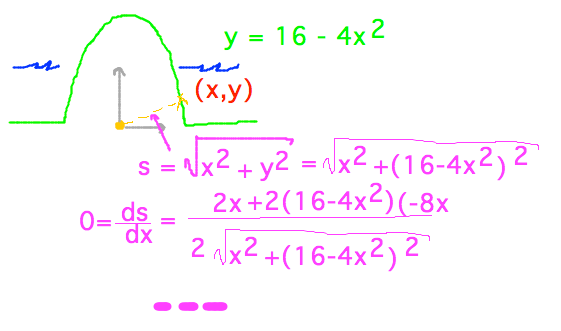
- Explorer at base of peninsula wants shortest route to shore
- Mean value theorem?
- Professor Ahab is obsessed with finding the “moby function,”
which has the properties that...
- M′(x) ≤ 1
- For any k, somewhere M(x+1) - M(x) ≥ k
- To show this can’t exist
- Pick some k > 1
- Know that somewhere M(x+1) - M(x) ≥ k
- Use Mean Value Theorem:
- ( M(x+1) - M(x) ) / ((x+1)-x) = M′(c) ≤ 1 from restriction on M′
- But ( M(x+1) - M(x) ) / ((x+1)-x) ≥ k > 1 from choice of k
- Professor Ahab is obsessed with finding the “moby function,”
which has the properties that...
- Related rates example
- End of section 5.2
- Riemann sums
- Subdivide interval [a,b] into subintervals of any width, make sums from this
- Choose n-1 points between x0 = a, x1, ... xn = b
- Partitions?

- Riemann formula
- Riemann sums
- “limit as norm(P) goes to 0 of Riemann sum”
- = limit as (maximum) width of subintervals goes to 0
- Implies a limit as number of subintervals goes to infinity
- Example infinite sum
- Get closed form for sum
- Take limit of closed form

- Definite integrals as Riemann sums
- Read section 5.3