- Examples
- Do manufacturers of buckets actually use dimensions that
come close to minimizing the amount of material needed to
make the bucket?
- Bucket = cylinder
- Surface area proportional to amount of plastic and cost
- = 2πrh + πr2
- Volume V = πr2h gives
- h = V/(πr2)
- So A = 2πrV/(πr2) + πr2
- = 2V/r + πr2
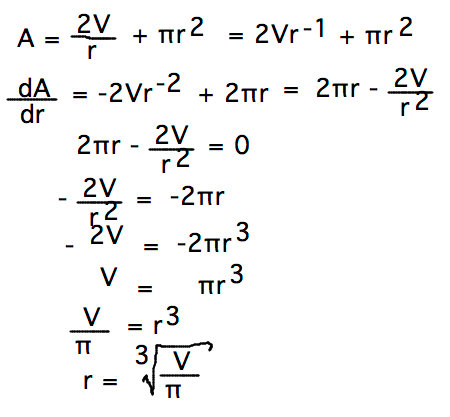
- = 2V/r + πr2
- Optimal r = (V/π)1/3
- V = 2.5 gallons = 577.5 cubic inches
> V = 2.5 * 231 > V [1] 577.5 > r = (V/pi)^(1/3) > r [1] 5.685919 > h = V / (pi*r^2) > h [1] 5.685919- Optimal r = 5.68, h = 5.68
- Actual r = 4.5, h = 10
- Optimal route for getting lawn mower back to shed.
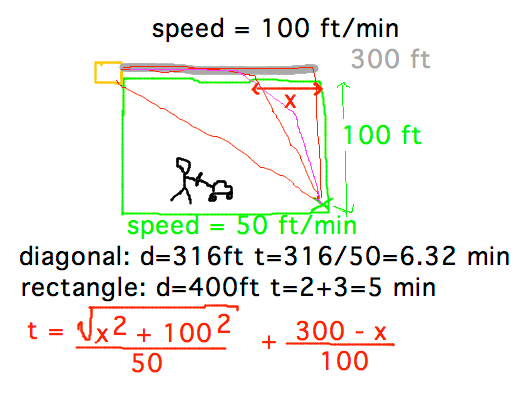
- Differentiate equation for time and find x that makes it 0

- Time for this x is less than times at endpoints of x interval, so optimal route crosses lawn to point 57.7 feet from end of driveway and then follows driveway
- Differentiate equation for time and find x that makes it 0
- Do manufacturers of buckets actually use dimensions that
come close to minimizing the amount of material needed to
make the bucket?
- Introduction to antiderivatives aka integrals
- Formalities
- Notation

- Rules (I added 2 re trigonometric antiderivatives that we didn’t mention in class)
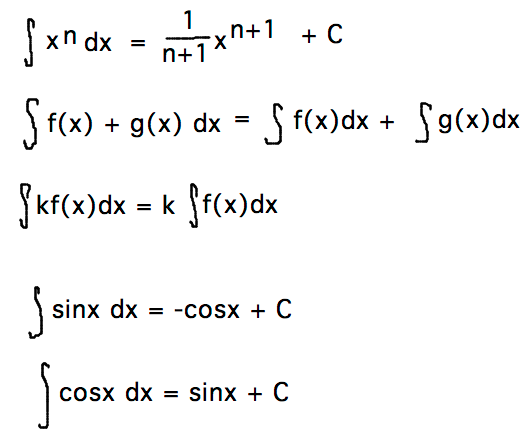
- Notation
- Formalities
- Antiderivative as a sum of function values
- Read section 5.1