- Date for hour exam 2 could be as early as Nov. 11
- Exam will cover material on derivatives since first exam (e.g., chain rule, implicit differentiation, related rates, extreme values, Mean Value Theorem, optimization, etc.)
- Open reference materials
- But harder, more word problems, than 1st test
- Figure out where f(x) = (x2+1) / x is increasing,
decreasing, (locally) maximum or minimum
- How does f′(x) compare to 0 (less, greater, equal)?
- f′(x) from quotient rule

- Section 4.4
- About concavity
- Concave up means derivative is increasing on open interval
- Concave down means derivative is decreasing
- 2nd derivative test for concavity
- 2nd derivative > 0 means concave up
- 2nd derivative < 0 means concave down
- Inflection point = point where function has tangent and concavity changes
- 2nd derivative test for extrema
- Derivative = 0, 2nd derivative < 0 means local max
- Derivative = 0, 2nd derivative > 0 means local min
- Derivative = 0, 2nd derivative = 0, test fails
- Curve sketching
- 2nd derivative tells you how 1st derivative is “curved” i.e., concavity
- Examples
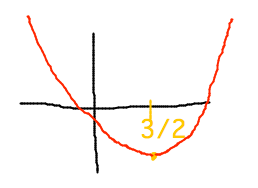
- f(x) = x2 - 3x + 1
- f′(x) = 2x - 3
- f′(x) = 0 implies x = 3/2
- f(3/2) = -5/4 = -1.25
- f′′(x) = 2
- Tabulate derivative information and intervals to which it applies
Interval f′() f′′() x < 3/2 - + x = 3/2 0 + x > 3/2 + + - 2nd derivative test says curve is concave up everywhere
- So critical point is a minimum
- Curve must look something like...
- g(x) = x2 + sin x
- g′(x) = 2x + cos x
- Find x such that 2x + cos x = 0
- cos x = -2x
- Calculator says x = -0.4502
- Only one max/min! I intuitively expected a parabola with
some oscillations superimposed by the sine function:

- ...But this seems not to happen—x2 presumably grows so fast it overwhelms the effects of sin x.
- g′′(x) = 2 - sin x
- 1 ≤ g′′(x) ≤ 3
- So now we know that this function is always concave up, and that the critical point at -0.4502 is a minimum
- f(x) = x2 - 3x + 1
- Partial algorithm for curve sketching
- Take derivatives
- Find critical points f/ 1st derivative
- Find intervals where 1st derivative is +, -
- Find intervals where 2nd derivative is +, -, or 0
- Find f(x) for key x values (critical points, x=0, etc.)
- Find zeros of f(x)
- See what more we can learn about x2 + sin x
- Optimization
- Read section 4.5