- Sign up to grade problem set
- “Treasure hunt” in sections 2.4 - 2.6
- What, precisely, does it take to make a function continuous at x = c?
- f continuous at c if continuous from left and from right and left limit = right limit
- limx→cf(x) = f(c)
- 3 conditions
- f(c) exists
- limx→cf(x) exists
- limx→cf(x) = f(c)
- Continuous on an interval?
- Continuous on interval [a,b] if
- Right-continuous at a
- Left-continuous at b
- Continuous at all other points in [a,b]
- Domain includes [a,b]
- Graph of f(x) over [a,b] has no breaks
- Example: hyperbola that is continuous on [0,n] but discontinuous on [-1,1]
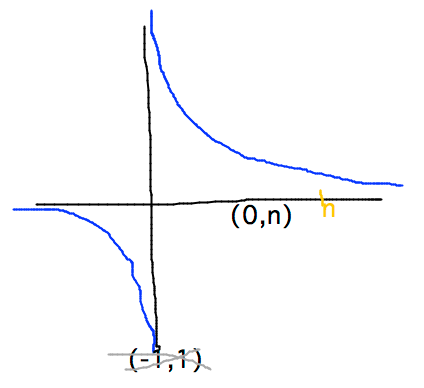
- Continuous on interval [a,b] if
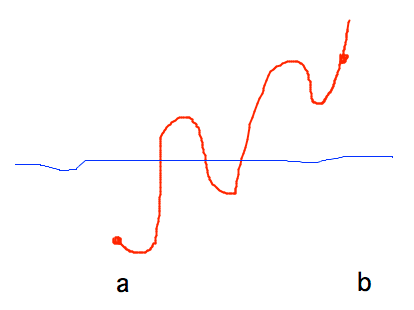
- What does the Intermediate Value Theorem say?
- Intermediate value property = continuous function that = a at one point and equals b at another takes on all values between a and b between those points
- Continuous function f(x) on [a,b], horizontal line between
f(a) and f(b) crosses graph of f
- What does it mean to talk about limx→±∞f(x)?
- Behavior as x gets arbitrarily big or arbitrarily small
- What does it mean to say that limx→cf(x) = ±∞?
- f(x) has vertical asymptote at c
- f(x) becomes arbitrarily large (or small) as x approaches c
- What is a 1-sided limit?
- Limit as x approaches c but from only above or below
- What is an asymptote?
- Value (line on graph) that function approaches as x approches ±∞ but never actually reaches
- b is (horizontal) asymptote for f(x) if limx→±∞f(x) = b
- Can also have vertical asymptotes where f(x) approaches ±∞
- What, precisely, does it take to make a function continuous at x = c?
- Examples
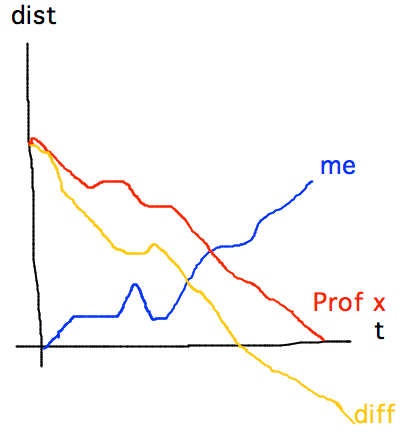
- Suppose I leave Geneseo at 8:00 some morning, driving to New
York City. At the same time Prof. X leaves Toronto driving to
Geneseo. Is there ever a time when I and Prof. X are exactly
the same distance from Geneseo (although in different places)?
Does the answer change if one or both of us stop, take detours,
backtrack, etc?
- Yes, there has to be a time at which we’re the same distance from Geneseo by intermediate value theorem
- No, backtracking etc doesn’t matter
- When can you “push” a limit inside a function application, i.e.,
when is limx→cf( g(x) ) = f( limx→cg(x) )?
Book theorem 10—when f is continuous at g(c)
- Can you find
limx→π/4cos( (x2-π2/16) / (x-π/4) )? How about
limx→π/4tan( (x2-π2/16) / (x-π/4) )?
- limx→π/4cos( (x2-π2/16) / (x-π/4) )
- = cos( limx→π/4(x2-π2/16) / (x-π/4) )
- = cos( limx→π/4(x-π/4)(x+π/4) / (x-π/4) )
- = cos( limx→π/4(x+π/4)
- = cos( π/2 )
- = 0
- The last few steps of this derivation as a drawing, if that’s more readable:
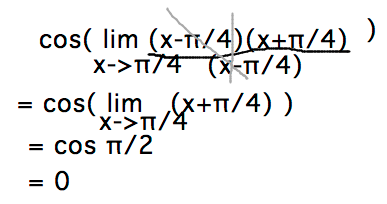
- Can you find
limx→π/4cos( (x2-π2/16) / (x-π/4) )? How about
limx→π/4tan( (x2-π2/16) / (x-π/4) )?
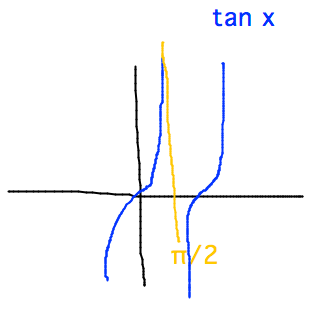
- Is limx→π/2tan x defined? (No, left and right limits differ.)
What about limx→π/2+tan x? (Yes, tangent approaches
-∞ for x > π/2.)
- Suppose I leave Geneseo at 8:00 some morning, driving to New
York City. At the same time Prof. X leaves Toronto driving to
Geneseo. Is there ever a time when I and Prof. X are exactly
the same distance from Geneseo (although in different places)?
Does the answer change if one or both of us stop, take detours,
backtrack, etc?
- Introduction to derivatives
- Section 3.2
- Limits and derivatives problem set