Limit Laws

Return to List of Lectures

Previous Lecture

• Questions?
• Limit Laws
  • “Limit Laws” part of section 2.2
    • Limit laws, for e.g., addition
      • Taking a limit distributes over +, -, multiplication, division, powers, roots
      • e.g., lim_x→c( f(x) + g(x) ) = lim_x→cf(x) + lim_x→cg(x)
    • Theorems, e.g., Sandwich Theorem?
      • Limit of polynomial
        • Polynomial is f(x) = a_nxⁿ + a_n-1x^n-1 + ... + a₁x + a₀
        • lim_x→c(a_nxⁿ + a_n-1x^n-1 + ... + a₁x + a₀)
          • = a_ncⁿ + a_n-1c^n-1 + ... + a₁c + a₀
        • Because of
          • Addition law
            • lim_x→c(a_nxⁿ + a_n-1x^n-1 + ... + a₁x + a₀)
            • = lim_x→ca_nxⁿ + lim_x→ca_n-1x^n-1 + ...
          • Constant multiple rule
            • lim_x→ca_nxⁿ + lim_x→ca_n-1x^n-1 + ...
            • = a_n lim_x→cxⁿ + a_n-1 lim_x→cx^n-1 + ...
          • Power law
            • a_n lim_x→cxⁿ + a_n-1 lim_x→cx^n-1 + ...
            • = a_n (lim_x→cx)ⁿ + a_n-1 (lim_x→cx)^n-1 + ...
            • = a_ncⁿ + a_n-1c^n-1 + ... + a₁c + a₀
      • Limit of rational function (ratio of 2 polynomials, p(x) & q(x))
        • lim_x→c( p(x) / q(x) ), given q(c) ≠ 0
          • = p(c) / q(c)
        • Because
          • Quotient rule
          • Limit of polynomial
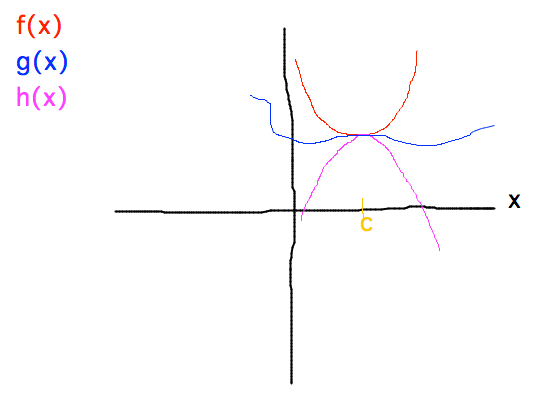
      • Sandwich Theorem?
        
  • Examples
    • lim_x→0( x cosx )
      • (at least) 2 ways of figuring this out, the first of which demonstrates Sandwich Theorem
        • -|x| ≤ x cosx ≤ |x| because -1 ≤ cos x ≤ 1
        • lim_x→0-|x| = lim_x→0|x| = 0
        • So Sandwich Theorem says lim_x→0( x cosx ) = 0
      • Or
        • lim_x→0( x cosx )
        • = lim_x→0(x) lim_x→0(cosx )
        • = 0 × 1 = 0
      • Or just plug x = 0 into x cosx
        • You can do this because x cosx is continuous around x = 0, i.e., has no breaks in its graph
          
        • If f(x) is continuous around c then lim_x→cf(x) = f(c)
        • But technically using continuity like this to find a limit is circular, because the definition of continuity is that the limit equals the function value—but as long as we’re doing limits intuitively, continuity is an easy property to recognize by intuition.
    • If lim_x→0f(x) = 3 and lim_x→0g(x) = 16, what is
      • lim_x→0( f(x) + g(x) )?
        • Sum rule: 3 + 16 = 19
      • lim_x→0( √g(x) )?
        • root rule: √16 = 4
• Definition of Limit
  • Think of idea of limit as where function seems to be heading across a small gap in its graph
  • If function heads for the same value no matter how small you make the gap, then that value is the limit
    
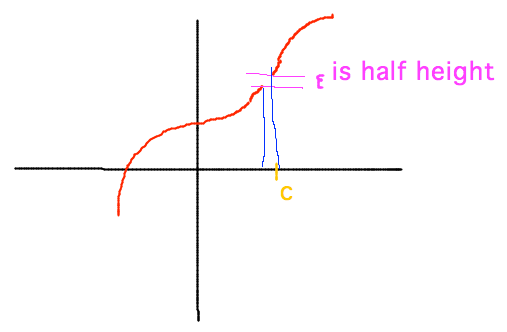
  • lim_x→cf(x) = L iff for any ε > 0 you can find a δ such that whenever 0 < | x - c | < δ, then 0 < | f(x)- L | < ε
• Next
  • More on the formal definition of limit
  • Section 2.3 (“The Precise Definition of a Limit”)

Next Lecture