SUNY Geneseo Department of Computer Science

Problem Set 2—Breadth First Search

Purpose

Background

Exercise

Solve each of the following problems.

Problem 1

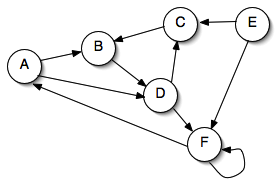
Carry out a breadth first search on the following graph by hand, showing the d and π values computed for every vertex. The source vertex for your search should be vertex A.

Problem 2

Problem 22.2-4 in the textbook. In addition to deriving the execution time of breadth first search driven by an adjacency matrix, show pseudocode for the modified algorithm.

Problem 3

Suppose you are given a graph, G, and two vertices in G, s and t. Your task is to find a shortest path from s to t, i.e., a path with a minimum number of edges. Give pseudocode for an algorithm that solves this problem. Output from the algorithm should be a list of edges on a shortest path from s to t, or nil if there is no path from s to t. Explain why your algorithm is correct (the explanation doesn’t have to be a rigorous proof though).

Problem 4

Problem 22.2-8 in our textbook asks for an algorithm that finds the diameter of a tree—see the book for the exact problem and definitions of terms. Phineas Phoole looks at this problem and reasons as follows: “Since we’re dealing with a tree, there is only one (simple) path between any pair of vertices. So if I pick any vertex as a starting point and then find two vertices on ‘opposite’ sides of it and as far away from it as possible, they must be the pair that is farthest apart in the whole tree, i.e., the pair that defines the tree’s diameter, i.e., the diameter is simply the sum of their distances from my starting vertex. And breadth first search can give me the distances from the starting vertex.”

In slightly more detail, Phineas’s proposed algorithm looks like this, where T is the (undirected) tree whose diameter is wanted:

    Pick any vertex from T, call that vertex s
    Run breadth first search on T with source vertex s
    For each child, c, of s in the breadth first tree constructed by the search
        Let dc be the largest d value on any vertex reachable from c (because T is a tree, vertices reachable
        from c are not reachable in any other way from s; dc can be computed via, e.g., a depth-first traversal
        of the subtree rooted at c)
    Let d1 and d2 be the 2 largest dc values found above
    Return d1 + d2

Show that Phineas’s algorithm does not in fact always work. (Hint: try to construct a proof that the algorithm does work, paying careful attention to the logic needed in that proof—somewhere the logic will break down, pointing you to the flaw in the algorithm.)

Follow-Up

I will grade this exercise in a face-to-face meeting with you. During this meeting I will look over your solutions, ask any questions I have about them, answer any questions you have, etc. Even though we will have a chance to talk about your solutions, please bring them in writing to the meeting—that will speed things along.

Each meeting should take about 15 minutes. Please schedule your meeting by signing up on the schedule sheet outside my office or electronically via Google calendar. If you work in a group on this exercise, the whole group can have a single meeting with me. Make sure that your meeting ends by the end of the day on the due date above.