SUNY Geneseo Department of Computer Science

Probability, Expectation, and Indicator Random Variables

Return to List of Lectures

Questions?

Table size and hash function

• No point in table being bigger than max value h() produces
• Hashing strings to get large hash codes

            h = 0
            for each character c in string
                h = ( h * 256 + c ) % tableSize        // Can also multiply c by its position and add to h

Java Scanners

Generally a scanner is something that breaks a stream of characters into “lexemes” (word-like units such as words, numbers, punctuation marks, etc.)

Demonstration program that reads words from a file and prints them

Probability

Appendix C.2 through discrete distributions, C.3 through expected value, and analysis of hashing with chaining in 11.2

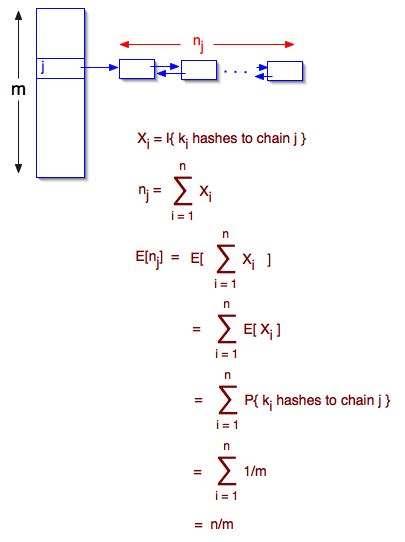
Indicator random variables

• Random variable whose values are 1 if some event happens and 0 if event doesn’t happen
  • Book’s example of an indicator for two keys hashing to the same chain: X_ij = I{ h(k_i) = h(k_j) }
• Expected value of an indicator random variable
  • E[ X ] = x1 p{X=x1} + x2 p{X=x2} + ... + xn p{X=xn}
  • E[ I{e} ] = 1 p{e} + 0 (1-p{e}) = p{e}
• Application: rigorously derive the expected length of a chain in a hash table
• n_j = length of chain j in hash table
• Intuitively, E[n_j] = n/m

Next

Analysis of hashing

• Review “Analysis of hashing with chaining” in section 11.2 (middle of page 258 through bottom of 260)

Backtracking review